Перед е Патерналізм теор е ми теорії ймовірностей, загальна назва ряду теорем ймовірностей теорії , Що вказують умови виникнення тих чи інших закономірностей в результаті дії великого числа випадкових чинників. Історично перші П. т. - теорема Бернуллі (1713) і теорема Лапласа (1812) - відносяться до розподілу відхилень частоти появи деякої події Е при n незалежних випробуваннях від його ймовірності р (0 <р <1). Частотою називається відношення m / n, де m - число наступів події Е при n випробуваннях (точні формулювання див. В ст. Бернуллі теорема і Лапласа теорема ). С. Пуассон (1837) розповсюдив ці теореми на випадок, коли ймовірність pk настання Е в k- м випробуванні може залежати від k, описавши граничну поведінку при n ® ¥ розподілу відхилень частоти m / n від середнього арифметичного 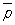ймовірностей pk (1 £ k £ n):

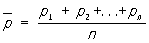
(Див. Великих чисел закон ). Якщо позначити через Xk випадкову величину, що приймає значення, рівне одиниці при появі події Е в k- м випробуванні, і значення, рівне нулю при його непояві, то m можна представити у вигляді суми

m = X1 + X2 + ... + Xn,

що дозволяє розглядати перераховані теореми як окремі випадки загальних П. т., що відносяться до сум незалежних випадкових величин (закону великих чисел і центральної граничної теореми).

Закон великих чисел. нехай

X1, X2, ..., Xn, ... (*)

- будь-яка послідовність незалежних випадкових величин, sn - сума перших n з них

sn = X1 + X2 + ... + Xn,

An і B2n - відповідно математичне очікування

An = Е sn = Е X1 + E X2 + ... + E Xn,

і дисперсія

B2n = D sn - = D X1 + D X2 + ... + D Xn,

суми sn. Кажуть, що послідовність (*) підкоряється закону великих чисел, якщо при будь-якому e> 0 вірогідність нерівності

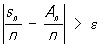
прямує до нуля при n ® ¥.

Широкі умови приложимости закону великих чисел знайдені вперше П. Л. Чебишева (В 1867) (див. Великих чисел закон ). Ці умови потім були узагальнені А. А. Марковим (Старшим). Питання про необхідні і достатні умови прикладеності закону великих чисел було остаточно вирішено А. Н. Колмогоровим (1928). У разі, коли величини Xn мають одну і ту ж функцію розподілу, ці умови, як показав А. Я. Хинчин (1929), зводяться до одного: величини Xn повинні мати кінцеві математичні очікування.

Центральна гранична теорема. Кажуть, що до послідовності (*) застосовна центральна гранична теорема, якщо при будь-яких z1 і z2 ймовірність нерівності

z1Bn <sn - An <z2Bn

має межею при n ® ¥ - величину

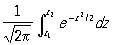
(Див. Нормальний розподіл ). Досить загальні достатні умови застосовності центральної граничної теореми були вказані Чебишевим (1887), а й в його доказі виявилися прогалини, заповнення лише пізніше Марковим (1898). Вирішення питання, близьке до остаточного, було отримано А. М. Ляпуновим (1901). Точне формулювання теореми Ляпунова така: нехай

ck = E | Xk - Е Хк | 2+ d, d> 0

Cn = c1 + c2 + ... + cn.

якщо відношення 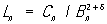прямує до нуля при n ® ¥, то до послідовності (*) застосовна центральна гранична теорема. Остаточне вирішення питання про умови приложимости центральної граничної теореми отримано в основних рисах С. Н. Бернштейном (1926) і доповнено В. Феллером (1935).

З ін. Напрямків робіт в області П. т. Можна відзначити наступні.

1) Розпочаті Марковим і продовжені Бернштейном і ін. Дослідження умов приложимости закону великих чисел і центральної граничної теореми до сум залежних величин.

2) Навіть в разі послідовності однаково розподілених випадкових величин можна вказати прості приклади, коли суми мають в межі розподіл, відмінне від нормального (мова йде про невироджених розподілах, т. Е. Про розподіли, що не зосереджених цілком в одній точці). У роботах радянських математиків А. Я. Хинчина, Б. В. Гнеденко, французьких математиків П. Леві, В. Дебліна і ін. Повністю вивчені як клас можливих граничних розподілі для сум незалежних випадкових величин, так і умови збіжності розподілів сум до того чи іншому граничного розподілу.

3) Значна увага приділяється т. Н. локальним П. т. Хай, наприклад, величини Xn приймають лише цілі значення. Тоді суми sn приймають також лише цілі значення і природно поставити питання про граничний поведінці ймовірностей Pn (m) того, що sn = m (де m - ціле). Найпростішим прикладом локальної П. т. Може служити локальна теорема Лапласа (див. Лапласа теорема ).

4) П. т. В їх класичній постановці описують поведінку окремої суми sn зі зростанням номера n. Досить загальні П. т. Для ймовірностей подій, залежних відразу від декількох сум, отримані вперше Колмогоровим (1931). Так, наприклад, з його результатів слід, що при досить широких умовах ймовірність нерівності

має межею величину

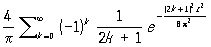(Z> 0)

5) Перераховані вище П, т. Відносяться до сум випадкових величин. Прикладом П. т. Іншого роду можуть служити П. т. Для членів варіаційного ряду . Ці П. т. Детально вивчені радянськими математиками Б. В. Гнеденко і Н. В. Смирновим.

6) Нарешті, до П. т. Відносять також і теореми, що встановлюють властивості послідовностей випадкових величин, що мають місце з ймовірністю, яка дорівнює одиниці (див., Наприклад, Повторного логарифма закон ).

Літ .: Гнеденко Б. В., Колмогоров А. Н., Граничні розподілу для сум незалежних випадкових величин, М. - Л., 1949; Ібрагімов І. А., Линник Ю. В., Незалежні і стаціонарно пов'язані величини, М., 1965; Прохоров Ю. В., Розанов Ю. А., Теорія ймовірностей. Основні поняття. Граничні теореми. Випадкові процеси, 2 видавництва., М., 1973.

Ю. В. Прохоров.