1. Визначення і формула коефіцієнта в'язкості ВИЗНАЧЕННЯ В'язкістю називають один з видів явищ переносу....
2. Коефіцієнт внутрішнього тертя газу
3. Коефіцієнт в'язкості рідин
4. Формула Пуазейля
5. число Рейнольдса
6. Одиниці виміру коефіцієнта в'язкості
7. Приклади розв'язання задач
8. Що таке в'язкість рідини?
9. Ньютонівські и неньютонівські середовища
10. Кров як внутрішнє середовище організму
11. Коефіцієнти в'язкості середовища
12. Методи визначення в'язкості рідини
13. Практичне застосування віскозиметра
14. Яку роль відіграє в'язкість в медичному обладнанні?
15. Висновок
16. Фактори, що впливають на в'язкість
17. Важливість для промисловості

Визначення і формула коефіцієнта в'язкості

ВИЗНАЧЕННЯ

В'язкістю називають один з видів явищ переносу. Вона пов'язана з властивістю текучих речовин (газів і рідин), чинити опір переміщенню одного шару відносно другого. Це явище викликається рухом частинок, які складають речовина.

Виділяють динамічну в'язкість і кінематичну.

Розглянемо рух газу, що володіє в'язкістю як переміщення плоских паралельних шарів. Будемо вважати, що зміна швидкості руху речовини відбувається в напрямі осі X, яка перпендикулярна до напрямку швидкості руху газу (рис.1).

У напрямку осі Y швидкість руху в усіх точках однакова. Значить, швидкість є функцією. В такому випадку, модуль сили тертя між шарами газу (F), яка діє на одиницю площі поверхні, яка розділяє два сусідніх шару, описується рівнянням:

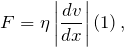
де - градієнт швидкості () по осі X. Вісь X перепендикулярно напрямку руху шарів речовини (рис.1).

визначення

Коефіцієнт (), що входить в рівняння (1) називається коефіцієнтом динамічної в'язкості (коефіцієнтом внутрішнього тертя ). Він залежить від властивостей газу (рідини). чисельно дорівнює кількості руху, яке переноситься в одиницю часу через майданчик одиничної площі при градієнті швидкості дорівнює одиниці, в напрямку перпендикулярному майданчику. Або чисельно дорівнює силі, яка діє на одиницю площі при градієнті швидкості, що дорівнює одиниці.

Внутрішньо тертя - причина того, що для течії газу (рідини) крізь трубу необхідна різниця тисків. При цьому, чим більше коефіцієнт в'язкості речовини, тим більше повинна бути різниця тисків для додання заданої швидкості течії.

Коефіцієнт кінематичної в'язкості зазвичай, позначають. Він дорівнює:

де - щільність газу (рідини).

Коефіцієнт внутрішнього тертя газу

Відповідно до кінетичної теорії газів коефіцієнт в'язкості можна обчислити за допомогою формули:

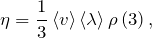
де - середня швидкість теплового руху молекул газу, - середня довжина вільного пробігу молекули. Вираз (3) показує, що при низом тиску (розріджений газ) в'язкість майже не залежить від тиску, так як 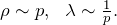Але такий висновок справедливий до моменту, поки відношення довжини вільного пробігу молекули до лінійним розмірам судини не стане приблизно рівним одиниці . При збільшенні температури в'язкість газів зазвичай зростає, так як

Коефіцієнт в'язкості рідин

Вважаючи, що коефіцієнт в'язкості визначено силами взаємодії молекул речовини, які залежать від середньої відстані між ними, то коефіцієнт в'язкості визначають експериментальної формулою Бачинського:

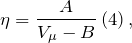
де - молярний об'єм рідини, А і B - постійні величини.

В'язкість рідин з ростом температури зменшується, при збільшенні тиску зростає.

Формула Пуазейля

Коефіцієнт в'язкості входить в формулу, яка встановлює залежність між обсягом (V) газу, який протікає в одиницю часу через перетин труби і необхідної для цього різницею тисків ():

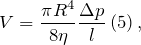
де - довжина труби, - радіус труби.

число Рейнольдса

Характер руху газу (рідини) визначається безрозмірним числом Рейнольдса ():

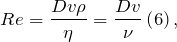
- величина, яка характеризує лінійні розміри тіла, обтічного рідиною (газом).

Одиниці виміру коефіцієнта в'язкості

Основною одиницею виміру коефіцієнта динамічної в'язкості в системі СІ є:

1Па c = 10 пуаз

Основною одиницею виміру коефіцієнта кінематичної в'язкості в системі СІ є:

Приклади розв'язання задач

ПРИКЛАД 1

Завдання Динамічно в'язкість води дорівнює Па с. Яка величина граничного діаметру труби дозволить течією води залишитися ламінарним, якщо за 1 с через поперечний переріз випливає обсяг води рівний? Рішення Умова ламінарності течії рідини має вигляд:

Де число Рейнольдса знайдемо за формулою:

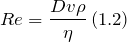
Швидкість течії води знайдемо як:

У вираженні (1.3) - висота водяного циліндра, що має об'єм:

Лабораторна робота №1

Визначення коефіцієнта в'язкості рідини методом Стокса. Дослідження залежності в'язкості рідини від температури

Коротка теорія

При русі рідини між її шарами виникають сили внутрішнього тертя, що діють таким чином, щоб зрівняти швидкості всіх шарів. Виникнення цих сил пояснюється тим, що шари, що рухаються з різними швидкостями , Обмінюються молекулами. Молекули з більш швидкого шару передають імпульс молекулам більш повільного, внаслідок чого повільний шар починає рухатися швидше. Молекули з більш повільного шару отримують імпульс в швидкому шарі, що призводить до його гальмування.

Розглянемо рідину, що рухається в напрямку осі Х (рис.1). Нехай шари рідини рухаються з різними швидкостями. На осі Z візьмемо дві точки, що знаходяться на відстані dz. Швидкості потоку відрізняються в цих точках на величину d υ. ставлення 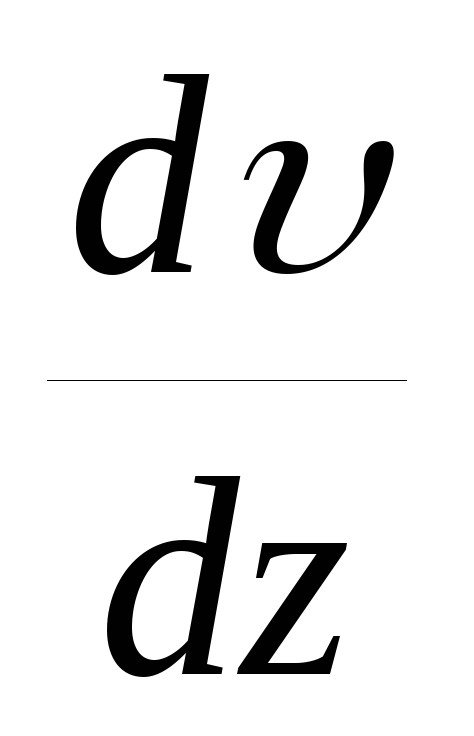характеризує зміну швидкості потоку в напрямку осі Z і називається градієнтом швидкості.

Сила внутрішнього тертя (сила в'язкості), що діє між двома дотичними шарами, пропорційна площі їхнього зіткнення і модулю градієнта швидкості:

.

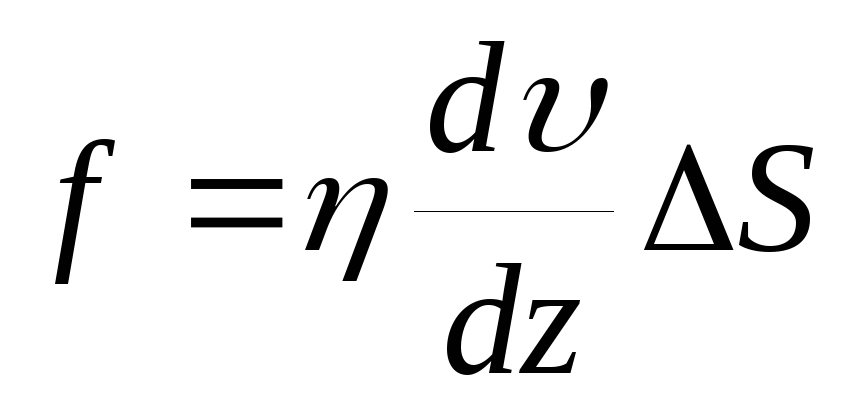Величина η називається коефіцієнтом динамічної в'язкості (внутрішнього тертя) або просто в'язкістю. Коефіцієнт в'язкості - це властивість текучого середовища чинити опір переміщенню однієї її шару відносно другого. Виходячи з формули, коефіцієнт динамічної в'язкості чисельно дорівнює силі внутрішнього тертя, що виникає на одиниці поверхні зіткнення двох шарів, що рухаються один відносно іншого з градієнтом швидкості, що дорівнює одиниці. В системі СІ коефіцієнт в'язкості має розмірність Па · с.

На всяке тіло, що рухається в в'язкої рідини, діє сила опору. У загальному випадку величина цієї сили залежить від багатьох факторів: від форми тіла, від в'язкості рідини, від характеру обтікання і т. Д. Стоксом було встановлено, що при ламінарному обтіканні тіл безмежної рідиною (т. Е. Коли опір середовища обумовлено практично тільки силами тертя) модуль сили опору визначається формулою:

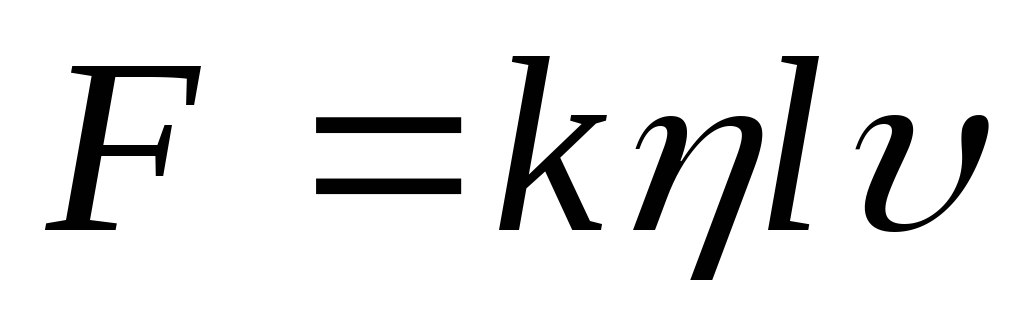, (1)

де υ - швидкість руху тіла, l - його характерний розмір, k - безрозмірний коефіцієнт, що залежить від форми тіла.

Гідродинамічний висновок формули (1) досить складний. Однак для отримання потрібного результату можна обмежиться аналізом завдання за допомогою теорії розмірностей. Перш ніж застосовувати теорію розмірностей, встановимо, виходячи з фізичних міркувань, від яких параметрів може залежати сила опору рідини. У нашому випадку, очевидно, такими параметрами є η, υ, l і щільність рідини ρ ж. Тоді, шуканий закон слід шукати у вигляді наступного статечного співвідношення:

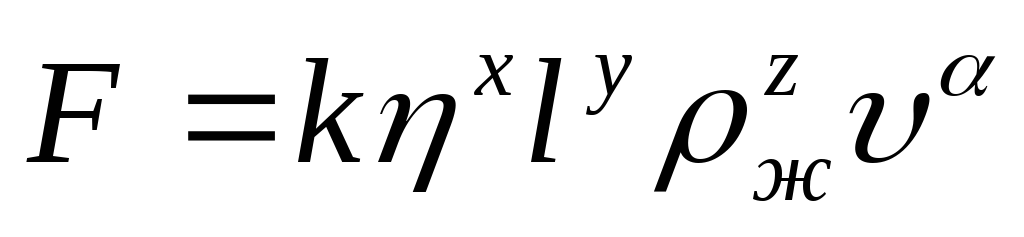, (2)

г 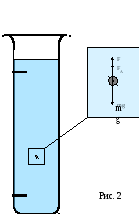деx, y, zі α - підлягають визначенню показники ступеня. Вони визначаються вимогою збіги размерностей лівої і правої частин останнього рівності. Оскільки розмірність виразу визначається ступенями при довжині, часу і масі, ми отримуємо три рівняння для знаходження чотирьох неізвестнихx, y, zі α. Поставлена ​​такий спосіб завдання однозначного рішення не має. Досвід показує, що при великих швидкостях руху (точніше кажучи, при великих числах Рейнольдса) сила опору пропорційна другий, а при малих швидкостях (малих числах Рейнольдса) - першого ступеня швидкості. Таким чином, при достатньо повільному русі можна покласти α = 1. Прирівнюючи показники ступеня при масі, довжині і часу в лівій і правій частинах рівняння, отримаємо систему трьох рівнянь з трьома невідомими, результатами вирішення якої є: x = 1, y = 1, z = 0. Підставивши отримані числа в співвідношення (2), отримаємо (1).

У разі ламінарного обтікання кульки безмежної рідиною Стоксом аналітично була отримана формула:

,

де r - радіус кульки. Як видно з останньої формули, коефіцієнт пропорційності k у випадку кульки дорівнює 6 π.

Виведемо рівняння руху довільного тіла, яке описує його вільне падіння всередині в'язкої рідини. Для виконання поставленого завдання запишемо другий закон Ньютона в проекції на вісь, направлену вертикально вниз (рис. 2):

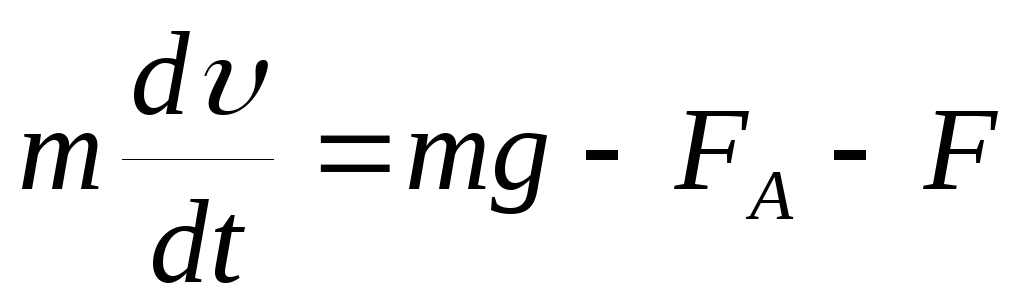, (3)

де m - маса тіла, g - прискорення вільного падіння, F A - сила Архімеда. Введемо щільність тіла ρ і його об'єм V. Виходячи з очевидних співвідношень m = ρ V, F A = ρ gV, застосовуючи формулу (1), з рівняння (3) отримаємо:

.

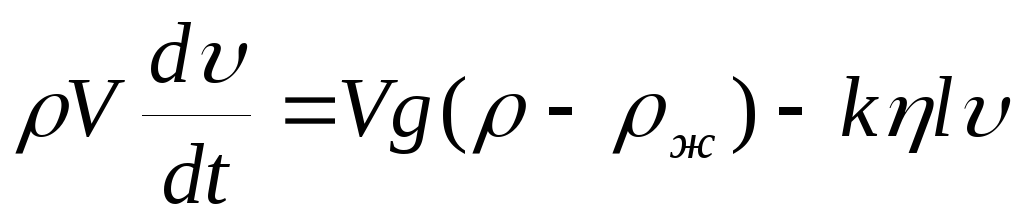Вирішуючи останнє рівняння, знайдемо:

У формулі (4) прийняті позначення: υ 0 - початкова швидкість кульки в рідині,

,
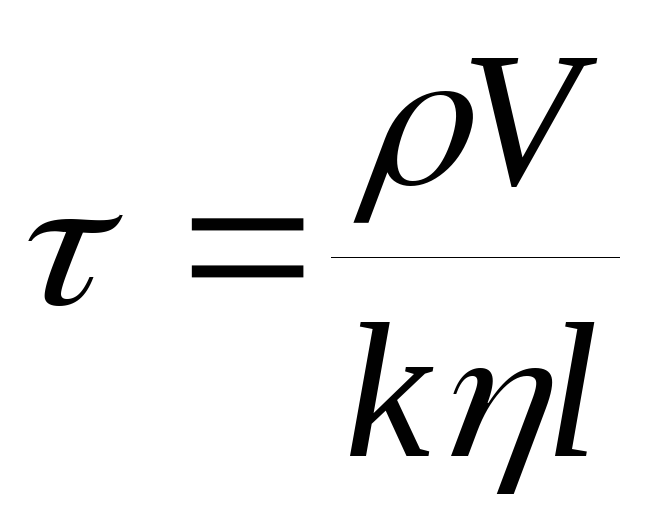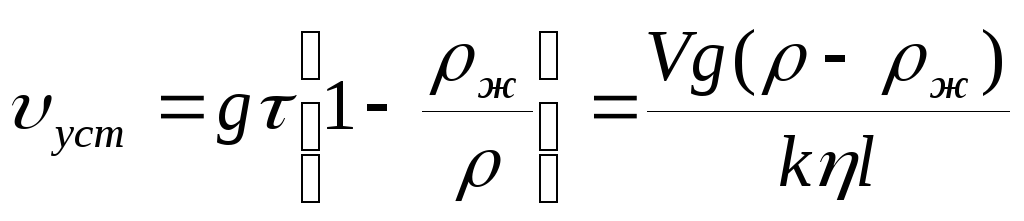. (5)

З формули (4) випливає, що швидкість падаючого тіла експоненціально наближається до сталої швидкості υ вуст. Те, наскільки швидко встановиться ця швидкість, визначається величиною τ, що має розмірність часу і називається часом релаксації. Якщо час падіння в кілька разів більше часу релаксації, то процес встановлення швидкості можна вважати закінченим.

У даній лабораторній роботі як падаючих тел будуть використовуватися кульки. Для кульок (врахувавши, що l = r і V = 4 / 3π r 3) формули (5) приймуть вигляд:

,
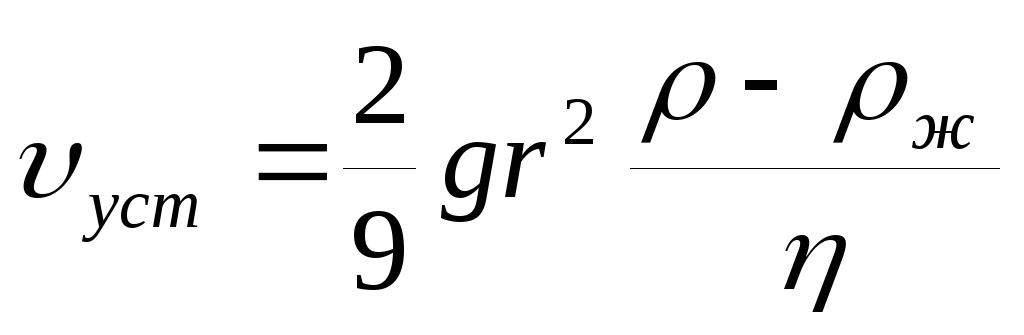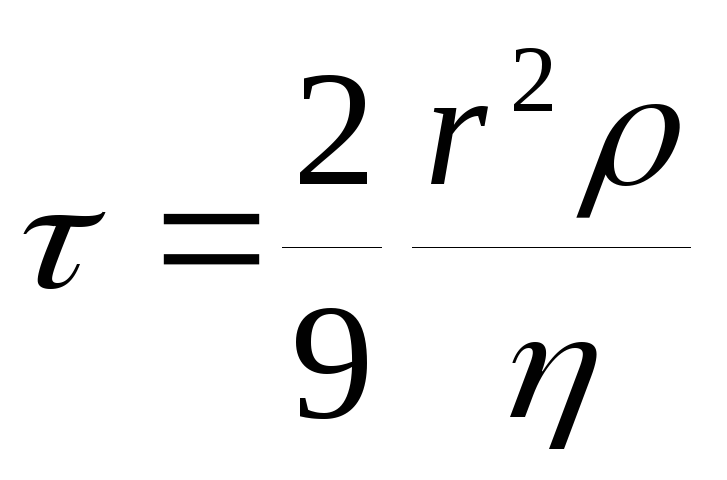. (6)

Вимірюючи на досвіді сталу швидкість падіння кульок υ вуст, можна визначити в'язкість рідини за формулою, наступної з (6):

. (7)

Володіючи способом експериментального визначення коефіцієнта в'язкості, можна досліджувати його залежність від зовнішніх чинників, зокрема, від температури. Досить очевидно, що при підвищенні температури в'язкість рідин зменшується. Для більш детального вивчення цього питання нам знадобиться розглянути молекулярну будову рідини.

У газах молекули рухаються хаотично, в їх розташуванні відсутній порядок. У кристалічних твердих тілах частинки коливаються близько певних положень рівноваги - вузлів кристалічної решітки. У рідинах, як і в кристалах, кожна молекула знаходиться в потенційній ямі електричного поля, створюваного оточуючими молекулами. Молекули коливаються із середньою частотою, близькою до частоти коливань атомів в кристалічних тілах (близько 10 12 Гц) і з амплітудою, яка визначається обсягом, наданим їй сусідніми молекулами. Глибина потенційної ями в рідинах більше середньої кінетичної енергії хитається молекули, тому молекули коливаються навколо більш-менш стабільних положень рівноваги. Однак, у рідин відмінність між цими двома енергіями невелика, так що молекули нерідко вискакують зі своєї потенційної ями і займають місце в інший.

Для того щоб перейти в новий стан, молекула повинна подолати ділянки з потенційною енергією, що перевищує середню теплову енергію молекул. Для цього теплова енергія молекул повинна - внаслідок флуктуації - збільшитися на деяку величину W, звану енергією активації. Чим більше енергія активації, тим рідше трапляються переходи молекул з одного положення рівноваги в інше.

Зазначений характер руху молекул пояснює як повільність дифузії в рідинах, так і велику (в порівнянні з газами) їх в'язкість. В основі явища в'язкості лежить перенесення молекулами імпульсу внаслідок теплового руху. Для того щоб привести в рух молекулу рідини необхідно (через наявність потенційної ями) передати їй більший імпульс, ніж у випадку з молекулою газу. Однак, кількість молекул, що мають енергії більше W, відповідно до формули Больцмана, експоненціально залежить від W. Чим меншою буде різниця між енергією активації і кінетичної енергією однієї молекули, тим більше буде кількість тих, на які не потрібно витрачати додаткову енергію, щоб вивести їх з потенційної ями. З підвищенням температури кількість подібних молекул буде зростати, отже, в'язкість рідини буде зменшуватися. Температурна залежність в'язкості рідини виражається формулою:

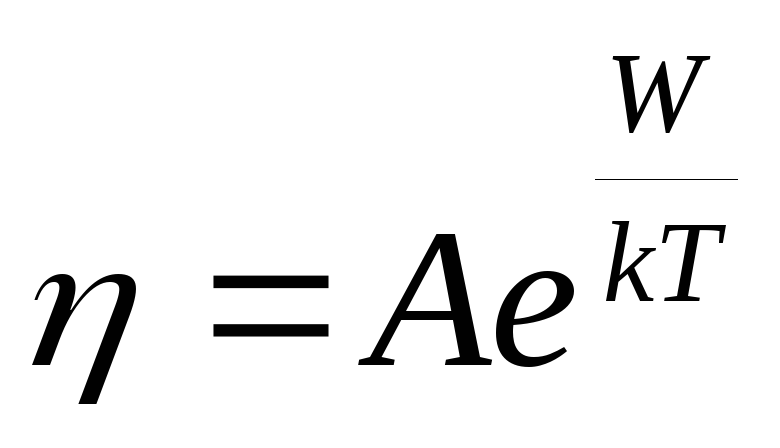. (8)

Формула (8) є логічним узагальненням всього вище сказаного.

Якщо прийняти, що при деякій температурі T 0 коефіцієнт в'язкості має значення η 0, то справедлива наступна запис:

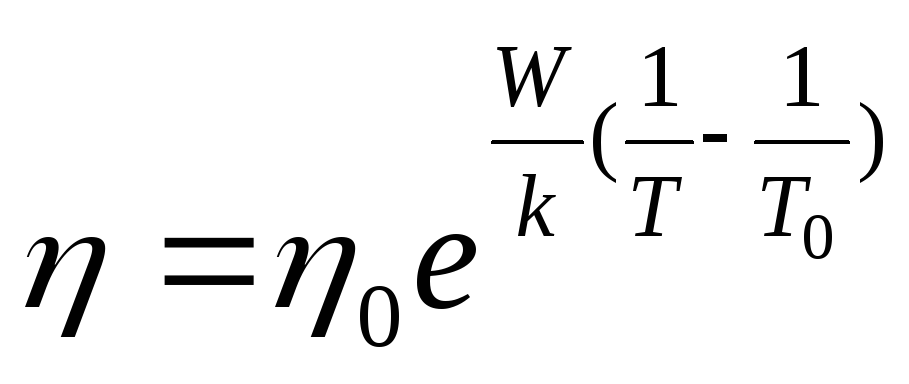, або

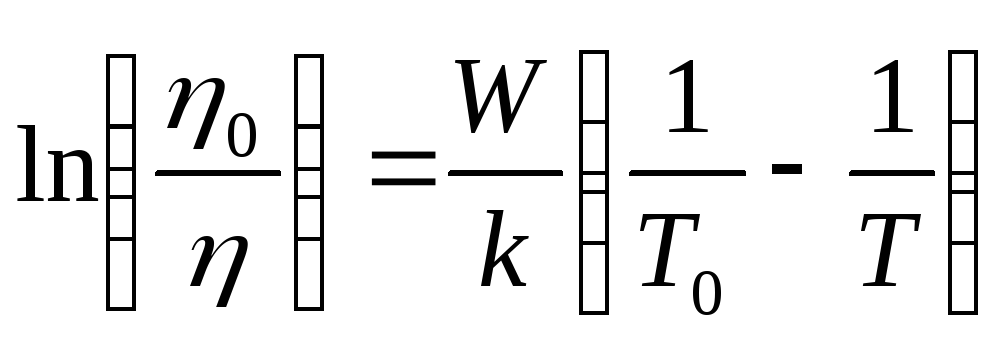. (9)

Якщо побудувати на графіку залежність величин ln (η 0 / η) і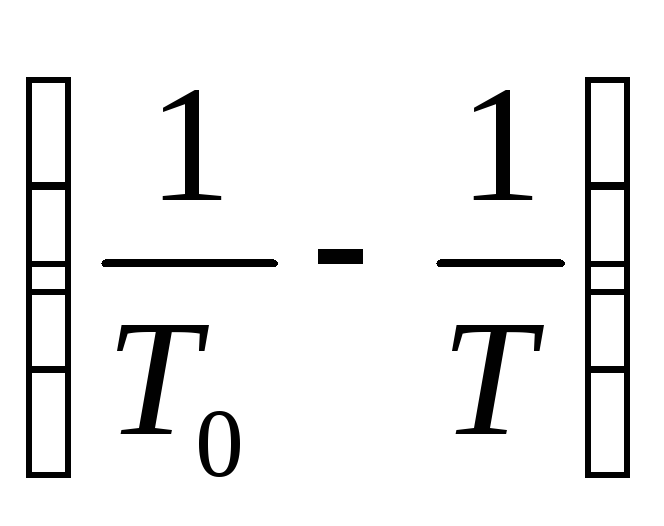
один від одного, то згідно з формулою (9) повинна вийти пряма лінія, по кутовому коефіцієнту якої можна визначити енергію активації молекули W досліджуваної рідини.

Експериментальна установка. Методика експерименту

Для вимірювань використовується скляний циліндричний посудину, наповнений досліджуваної рідиною (гліцерин). На стінках посудини нанесені дві мітки на деякій відстані один від одного. Верхня мітка повинна розташовуватися нижче рівня рідини з таким розрахунком, щоб швидкість кульки до моменту проходження цієї мітки встигала встановитися. Вимірюючи відстань між мітками за допомогою лінійки, а час падіння за допомогою секундоміра, визначають швидкість кульки υ вуст. За допомогою формули (7) обчислюється в'язкість. Радіуси кульок вимірюються мікрометром. Для кожної кульки рекомендується виміряти кілька різних діаметрів і обчислити середнє значення. Таке усереднення доцільно, оскільки в роботі використовуються кульки, форма яких може відрізнятися від сферичної. Щільності кульок і рідини беруться з таблиць.

Результати досвіду має сенс обробляти лише в тому випадку, якщо обтікання кульки рідиною має ламінарний характер. Характер обтікання можна визначити значенням числа Рейнольдса:

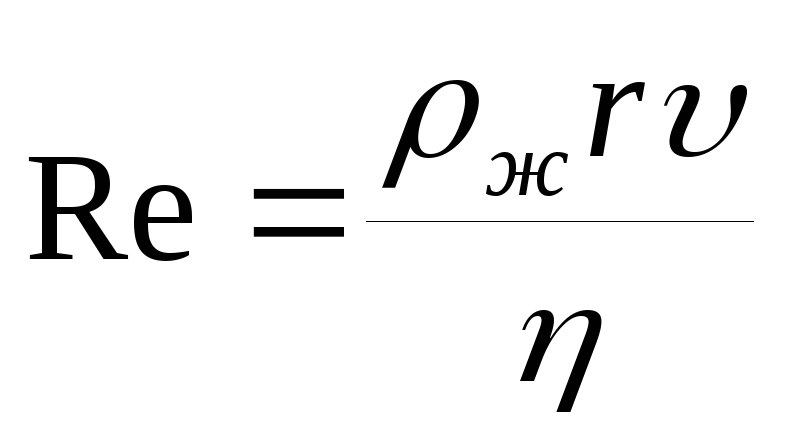. (10)

Обтікання є ламінарним лише при не дуже великих значеннях Re (Re 10).

Посудина з досліджуваної рідиною поміщений в термостат. Термостат є водяну ванну з нагрівачами. Для перемішування води в термостат подається повітря. від компресора. Компресор повинен бути включений під час роботи термостата. Для контролю за температурою досліджуваної рідини і води в термостаті служить ртутний термометр.

Дану лабораторну роботу формально можна розділити на дві частини.

У першій частині пропонується визначити коефіцієнт в'язкості при постійній температурі, використовуючи 4-5 кульок одного діаметра.

У другій частині роботи пропонується визначити вид температурної залежності коефіцієнта в'язкості (переконатися в справедливості формули (8)). Для цього, підігріваючи (охолоджуючи) воду в термостаті в інтервалі 20-60 о С, слід виконати вимірювання для 5-6 різних значень температури. Для окаждого значення температури рекомендується проводити 1-2 вимірювання . За результатами вимірювань будується графік завісімостіln (η 0 / η) від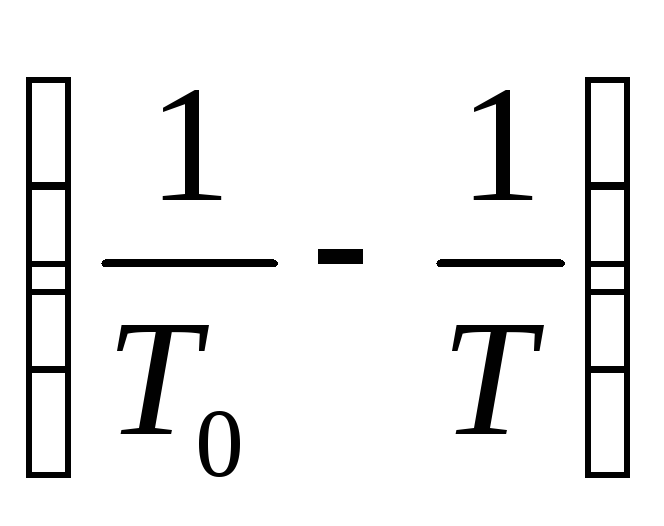
Якщо точки графіка лягають на одну пряму, то по її кутовому коефіцієнту, виходячи з формули (9), можна визначити значення енергії активації для даної рідини.

Вимірювання. Обробка результатів вимірювань

1. Відберіть 4-5 кульок одного діаметра.

2. Для однієї і тієї ж температури T 0 визначте встановилися швидкості падіння кульок і обчисліть коефіцієнт в'язкості. Оцініть похибку отриманого результату.

3. Увімкніть нагрівач в термостаті. Для 5-6 значень температури з інтервалу 20-60 о С зробіть виміри, кидаючи по 1-2 кульки. Результати вимірювань занесіть в таблицю. Обчисліть значення коефіцієнтів в'язкості для різних температур.

4. Для кожного з дослідів визначте значення числа Рейнольдса Re (формула (10)) та оцініть час релаксації τ (формула (6)).

5. Побудуйте графіки залежності коефіцієнта в'язкості від температури  (t) іln (η 0 / η) від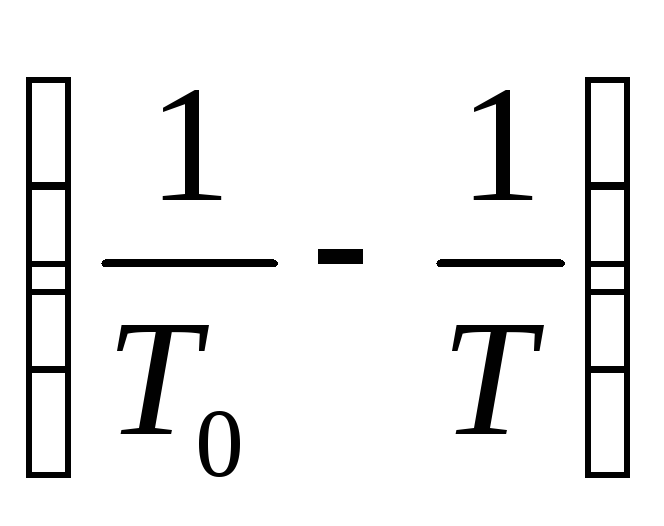
. За кутовому коефіцієнту прямої визначте енергію активації.

Додаткові питання:

Що таке в'язкість? В яких одиницях вимірюється коефіцієнт в'язкості?

Використовуючи теорію розмірності, отримаєте формулу (1). Чи має доказову силу цей висновок?

Які сили діють на кульку, що падає в рідині?

Як змінюється швидкість руху кульки зі збільшенням його діаметра?

У промисловості, наукової діяльності часто необхідно обчислити коефіцієнт в'язкості рідини. Робота зі звичайними або дисперсними середовищами у вигляді аерозолів, газових емульсій вимагає знань про фізичні властивості цих речовин.

Що таке в'язкість рідини?

Ще Ньютон започаткував таку науці, як реологія. Ця галузь займається вивченням опору речовини при русі, т. Е. В'язкості.

У рідинах і газах відбувається безперервна взаємодія молекул. Вони вдаряються одна об одну, відштовхуються або просто пролітають повз. В результаті шари речовини як би взаємодіють один з одним, надаючи швидкість кожного з них. Явище подібного взаємодії молекул рідин / газів і називається в'язкістю, або внутрішнім тертям.

Щоб краще розглянути цей процес, необхідно продемонструвати досвід з двома пластинками, між якими знаходиться рідка середу. Якщо рухати верхню пластинку, то «прилип» до неї шар рідини також почне рухатися з певною швидкістю v1. Через короткий проміжок часу помічаємо, що нижні шари рідини також починають рухатися по тій же траєкторії зі швидкістю v2, v3 ... vn і т. Д., Причому v1> v2, v3 ... vn. Швидкість самого нижнього з них залишається дорівнює нулю.

На прикладі газу такий досвід провести практично неможливо, т. К. Сили взаємодії молекул один з одним дуже малі, і візуально це зареєструвати не вдасться. Тут теж говорять про шарах, про швидкість руху цих шарів, тому в газоподібних середовищах також існує в'язкість.

Ньютонівські и неньютонівські середовища

Ньютоновская рідина - це така рідина, в'язкість якої можна вирахувати за допомогою формули Ньютона.

До таких середовищ відносяться вода і розчини. Коефіцієнт в'язкості рідини в таких середовищах може залежати від таких факторів, як температура, тиск або будова атома речовини, проте градієнт швидкості завжди залишиться незмінним.

Неньютонівські рідини - це такі середовища, в яких згадана вище значення може змінюватися, а значить, формула Ньютона тут діяти не буде. До таких речовин відносяться всі дисперсні середовища (емульсії, аерозолі, суспензії). Сюди ж відноситься і кров. Про це більш детально поговоримо далі.

Кров як внутрішнє середовище організму

Як відомо, 80% крові становить плазма, яка має рідке агрегатний стан, а решта 20% - це еритроцити, тромбоцити, лейкоцити і різні включення . Еритроцити людини мають діаметр 8 нм. У нерухомому стані вони формують агрегати у вигляді монетних стовпчиків, при цьому істотно підвищують в'язкість рідини. Якщо потік крові активний, ці «конструкції» розпадаються, а внутрішнє тертя, відповідно, зменшується.

Коефіцієнти в'язкості середовища

Взаємодія шарів середовища один на одного позначається на характеристиках всієї системи рідини або газу. В'язкість - це один із прикладів такого фізичного явища, як тертя. Завдяки їй верхні і нижні шари середовища поступово вирівнюють швидкості свого струму, і в кінцевому підсумку вона прирівнюється до нуля. Також в'язкість можна характеризувати як опір одного шару середовища іншому.

Для опису таких явищ виділяють дві якісні характеристики внутрішнього тертя:

• динамічний коефіцієнт в'язкості (динамічна в'язкість рідини);
• кінетичний коефіцієнт в'язкості (кінетична в'язкість).

Обидві величини пов'язані рівнянням υ = η / ρ, де ρ - щільність середовища, υ - кінетична в'язкість, а η - динамічна в'язкість.

Методи визначення в'язкості рідини

Віскозиметрія - це вимір в'язкості. На сучасному етапі розвитку науки знайти значення в'язкості рідини практичним шляхом можна чотирма способами:

1. Капілярний метод. Для його проведення необхідно мати дві посудини, з'єднаних скляним каналом невеликого діаметра зазвичай задовгі. Також потрібно знати значення тиску в одній посудині і в іншому. Рідина поміщається в скляний канал, і за певний проміжок часу вона перетікає з однієї колби в іншу.

Подальші підрахунки проводяться за допомогою формули Пуазейля для знаходження значення коефіцієнта в'язкості рідини.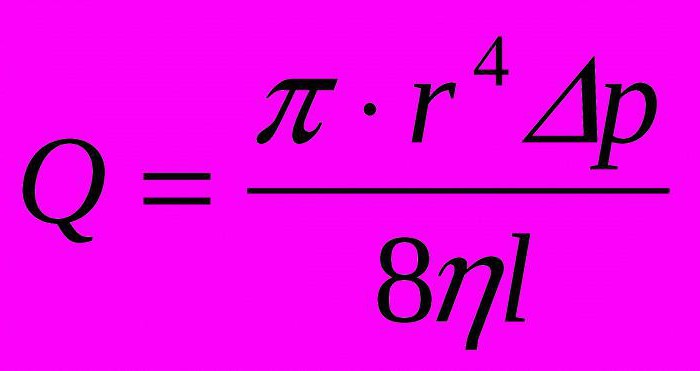

На практиці рідкі середовища можуть являти собою розпечені до 200-300 градусів суміші. Звичайна скляна трубка в таких умовах просто б деформувалася або навіть лопнула, що неприпустимо. Сучасні капілярні віскозиметри зібрані з якісного і стійкого матеріалу, який легко переживає такі навантаження.

2. Медичний метод по Гессе. Щоб розрахувати в'язкість рідини таким способом, необхідно мати не одну, а дві ідентичні капілярні установки. В одну з них поміщають середу з заздалегідь відомим значенням внутрішнього тертя, а в іншу - досліджувану рідину. Далі вимірюють два значення часу і складають пропорцію, по якій виходять на потрібне число.

3. Ротаційний метод. Для його проведення необхідно мати конструкцію з двох співвісних циліндрів. Це означає, що один з них повинен бути всередині іншого. У проміжок між ними заливають рідину, а потім надають швидкість внутрішньому циліндру. Ця кутова швидкість також повідомляється рідини. Різниця в силі моменту дозволяє обчислити в'язкість середовища.

4. Визначення в'язкості рідини методом Стокса. Для проведення цього досвіду необхідно мати вискозиметр Гепплера, який являє собою циліндр, заповнений рідиною. Перед початком експерименту роблять дві позначки на циліндрі і вимірюють довжину між ними. Потім беруть кульку певного радіуса R і опускають його в рідку середу. Щоб визначити швидкість його падіння, знаходять час пересування об'єкта від однієї мітки до іншої. Знаючи швидкість руху кульки, можна обчислити в'язкість рідини.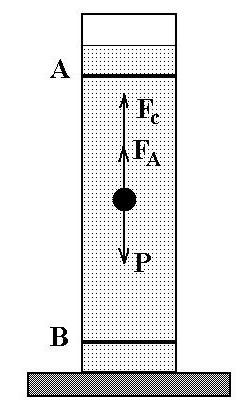

Практичне застосування віскозиметра

Визначення в'язкості рідини має велике практичне значення в нафтопереробній промисловості. При роботі з багатофазними, дисперсними середовищами важливо знати їхні фізичні властивості, особливо внутрішнє тертя. Сучасні віскозиметри зроблені з міцних матеріалів, при їх виробництві задіяні передові технології. Все це в сукупності дозволяє працювати з високій температурі і тиском без шкоди для самого обладнання.

В'язкість рідини відіграє велику роль в промисловості, тому що транспортування, переробка і видобуток, наприклад, нафти залежать від значень внутрішнього тертя рідинної суміші.

Яку роль відіграє в'язкість в медичному обладнанні?

Надходження газової суміші через ендотрахеальну трубку залежить від внутрішнього тертя цього газу. Зміна значень в'язкості середовища тут по-різному відбивається на проникненні повітря через апарат і залежить від складу газової суміші.

Введення лікарських препаратів, вакцин через шприц теж є яскравим прикладом дії в'язкості середовища. Йдеться про перепадах тиску на кінці голки при уприскуванні рідини, хоча спочатку вважали, що цим фізичним явищем можна знехтувати. Виникнення високого тиску на наконечнику - це результат дії внутрішнього тертя.

Висновок

В'язкість середовища - це одна з фізичних величин , Яка має велике практичне застосування. У лабораторії, промисловості, медицині - у всіх цих сферах поняття внутрішнього тертя фігурує дуже часто. Робота найпростішого лабораторного обладнання може залежати від ступеня в'язкості середовища, яка використовується для досліджень. Навіть переробна промисловість не обходиться без знань в галузі фізики.

В'язкість рідини може бути виміряна кількома способами за допомогою пристроїв, званих вискозиметрами. Такі прилади вимірюють час, витрачений речовиною на переміщення або час, необхідний об'єкту з заданим розміром і щільністю пройти через рідину. Одиницями виміру для цього параметра є Паскаль в квадраті.

Фактори, що впливають на в'язкість

Як правило, рідини, що складаються з великих молекул, будуть мати більш високу в'язкість. Особливо гостро це проявляється на прикладі довгих ланцюгових речовин, які є полімерами або важчими вуглеводневими сполуками. Такі молекули, як правило, перекривають один з одного, перешкоджаючи руху через них.

Іншим важливим фактором є те, як молекули взаємодіють один з одним. Полярні сполуки можуть утворювати водневі зв'язки, які утримують окремі молекули разом, збільшуючи загальний опір потоку або руху. Хоча молекула води і є полярною, вона має низьку в'язкість в зв'язку з тим, що її молекули досить малі. найбільш в'язкі рідини , Як правило, ті, які мають розтягнуті молекули або сильну полярність. Прикладами можуть служити гліцерин і пропіленгліколь.

Температура дуже впливає на в'язкість. Вимірювання властивостей рідин завжди даються в залежності від температури. У рідинах в'язкість зменшується з ростом температури. Це можна бачити при нагріванні сиропу або меду. Так відбувається тому, що молекули рухаються швидше і, отже, менше часу контактують один з одним. В'язкість газів, навпаки, збільшується з ростом температури. Це відбувається тому, що молекули рухаються швидше і відбувається більше зіткнень між ними. Таким чином збільшується щільність потоку.

Важливість для промисловості

Сира нафта часто переміщається на великі відстані між регіонами з різною температурою . Тому швидкість потоку і тиск змінюється з плином часу. Нафта, яка тече через Сибір, є більш вузький, ніж нафта в трубопроводах Перської затоки. У зв'язку з відмінностями в температурі зовнішнього середовища різними повинні бути і тиску в трубах, щоб змушувати її текти. Для вирішення цієї проблеми в труби спочатку заливається спеціальне масло, яке володіє практично нульовим коефіцієнтом внутрішнього опору. Таким способом обмежується контакт нафти з внутрішньою поверхнею труб. В'язкість масла також змінюється при перепаді температури. Щоб поліпшити його характеристики в масло додають полімери, які перешкоджають його загустіння і змішування з нафтою.

Параметр в'язкості виступає одним з основних властивостей визначають характер руху рідини.

В'язкість (внутрішнє тертя) рідини - властивість рідини чинити опір переміщенню однієї її частини щодо іншої. В'язкість рідини обумовлена ​​в першу чергу міжмолекулярним взаємодією, що обмежує рухливість молекул.

Якщо поточна рідина стикається з нерухомою поверхнею (наприклад при русі рідини в трубці) то шар такої рідини переміщається з різними швидкостями . В результаті між цими шарами виникає напруга зсуву: швидший шар прагне витягнутися в поздовжньому напрямку, а більш повільний затримує його.

Наявність в'язкості призводить до розсіювання (дисипації) енергії зовнішнього джерела, що викликає рух рідини, і переходу її в теплоту. Рідина без в'язкості (так звана ідеальна рідина) є абстракцією. Всім реальним рідин властива в'язкість.

Основний Закон в'язкої течії був встановлений І. Ньютоном (1687 г.) - формула Ньютона:

де F [Н] - сила внутрішнього тертя (в'язкості), що виникає між шарами рідини при зсуві їх відносно один одного; h | [Па-с] - коефіцієнт динамічної в'язкості рідини, що характеризує опір рідини зміщення її шарів; dV / dz - градієнт швидкості, що складає, скільки змінюється швидкість V при зміні на одиницю відстані в напрямку Z при переході від шару до шару, інакше-швидкість зсуву; S [м 2] - площа дотичних шарів.

Таким чином сила внутрішнього тертя гальмує більш швидкі шари і прискорює повільніші шари. Поряд з коефіцієнтом динамічної в'язкості розглядають так званий коефіцієнт кінематичної в'язкості

де r - щільність рідини.

Рідини діляться по вузькому властивостями на два види: ньютонівські і неньютонівські.

Ньютонівської називається рідина, коефіцієнт в'язкості якої залежить тільки від її природи і температури. Для ньютонівських рідин сила в'язкості прямо пропорційна градієнту швидкості. Для них безпосередньо справедлива формула Ньютона (9.1), коефіцієнт в'язкості в якій є постійним параметром, не залежних від умов перебігу рідини.

Неньютонівської називається рідина, коефіцієнт в'язкості якої залежить не тільки від природи речовини і температури, але також і від умов перебігу рідини, зокрема від градієнта швидкості. Коефіцієнт в'язкості в цьому випадку не є константою речовини. При цьому в'язкість рідини характеризують умовним коефіцієнтом в'язкості, який відноситься до певних умов перебігу рідини (наприклад, тиск, швидкість). Залежність сили в'язкості від градієнта швидкості стає нелінійної:

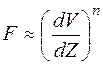(9.1, а)

де n характеризує механічні властивості при даних умовах
течії.

Прикладом неньютоновскіх рідин є суспензії. Якщо є рідина, в якій рівномірно розподілені тверді невзаимодействующие частки, то таке середовище можна розглядати як однорідну, тобто ми цікавимося явищами, що характеризуються відстанями, великими в порівнянні з розміром частинок. Властивості такого середовища в першу чергу залежать від в'язкості рідини. Система ж в цілому буде мати вже інший, більшої в'язкістю h ¢ залежить від форми і концентрації частинок. Для випадку малих концентрацій частинок З справедлива формула:

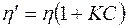(9.2)

де К - геометричний фактор - коефіцієнт, що залежить від геометрії частинок (їх форми, розмірів).

Якщо структура частинок зміниться (наприклад, при зміні умов перебігу), то і коефіцієнт К в (9.2), а отже, і в'язкість такої суспензії h "також зміниться. Подібна суспензія являє собою неньютонівської рідина. Збільшення в'язкості всієї системи пов'язано з тим, що робота зовнішньої сили при перебігу суспензій витрачається не тільки на подолання істинної (неньютоновской) в'язкості, обумовленої міжмолекулярним взаємодією в рідини, але і на подолання взаємодії між нею і структурними елементами.

Кров - неньютоновская рідина. Найбільшою мірою це пов'язано з тим, що вона володіє внутрішньою структурою, представляючи собою суспензію формених елементів в розчині - плазмі. Плазма - практично ньютоновская рідина. Оскільки 93% формених елементів складають еритроцити, то при спрощеному розгляді кров - це суспензія еритроцитів у фізіологічному розчині.

Характерною властивістю еритроцитів є, той факт, що при низьких швидкостях зсуву в крові утворюються агрегати еритроцитів у вигляді монетних стовпчиків. Ці агрегати розпадаються в міру збільшення швидкості зсуву, і тому ефективна в'язкість знижується. Максимальне напруження зсуву характеризує міцність безперервної агрегаційної структури в усій масі крові. Рівень напруги (зазвичай близько 0,005 н / м -2 залежить від показника гематокриту).

Умови освіти агрегатів різні в великих і дрібних судинах. Це пов'язано в першу чергу зі співвідношенням розмірів судини, агрегату і еритроцита характерні розміри d ер = 8 мкм, d агр »10d ер:

1. Великі судини (аорта, артерії):

Діаметр судини більше діаметра агрегату і значно діаметра еритроцита. При цьому градієнт швидкості зсуву невеликий, еритроцити збираються в агрегати у вигляді монетних стовпчиків. В цьому випадку в'язкість крові h = 0,005 Па с.

2. Дрібні судини (дрібні артерії, артеріоли):

Діаметр судини менше діаметра агрегату і більше в 5-20 діаметра еритроцита

У них градієнт швидкості зсуву значно збільшується і агрегати розпадаються на окремі еритроцити, тим самим зменшуючи в'язкість системи. Для цих судин чим менше діаметр просвіту, тим менше в'язкість крові. В судинах діаметром близько 5 d ер в'язкість крові становить приблизно 2/3 в'язкості крові у великих судинах.

3. мікросудин (капіляри):

Діаметр судини менше діаметра еритроцита

В живому посудині еритроцити легко деформуються, стаючи схожими на купол, і проходять, не руйнуючись, через капіляри навіть діаметром 3 мкм. В результаті поверхня дотику еритроцитів зі стінкою капіляра збільшується в порівнянні з недеформованому еритроцитом, сприяючи обмінним процесам.

Якщо припустити, що у випадках 1 і 2 еритроцити не деформуються, то для якісного опису зміни в'язкості системи можна застосувати формулу (9.2), в якій можна врахувати відмінність геометричного фактора для системи з агрегатів (К) і для системи окремих еритроцитів (К): до Ф К, що обумовлює відмінність в'язкості крові в великих і дрібних судинах.

Для опису процесів в мікросудинах формула (9.2) не може бути застосована, так як в цьому випадку не виконуються допущення про однорідність середовища і твердості частинок.

Таким чином, внутрішня структура крові, а отже, і її в'язкість (9.2), виявляється неоднаковою уздовж кровоносноїрусла в залежності від умов перебігу. Кров є неньютоновской рідиною. Залежність сили в'язкості від градієнта швидкості для течії крові по судинах не підкоряється формулою Ньютона (9.1) і є нелінійної.

В'язкість, характерна для течії крові у великих судинах: у нормі h = (4,2 - 6) Т) ^; при анемії h = (2 - 3) h в, при поліцитемії h = (15-20) h в. В'язкість плазми h пл == 1h в .. в'язкість води h в. = 0,01 Пуаз (1 Пуаз = 0,1 Па с).

Як і у будь-якої рідини, в'язкість крові зростає при зниженні температури. Наприклад, при зменшенні температури з 37 ° до 17 ° в'язкість крові зростає на 10%.