Термодін а міка, наука про найбільш загальні властивості макроскопічних систем, що знаходяться в стані термодинамічної рівноваги, і про процеси переходу між цими станами. Т. будується на основі фундаментальних принципів (почав), які є узагальненням численних спостережень і виконуються незалежно від конкретної природи утворюють систему тел. Тому закономірності в співвідношеннях між фізичними величинами, до яких призводить Т., мають універсальний характер. Обгрунтування законів Т., їх зв'язок з законами руху часток, з яких побудовані тіла, дається статистичною фізикою . Остання дозволяє з'ясувати і межі застосування Т.

Рівноважні і нерівноважні стану. Рівноважним є такий стан ізольованої системи, в яке вона переходить після закінчення, строго кажучи, нескінченно великого проміжку часу. Практично рівновага досягається за кінцевий час (час релаксації ), Яке залежить від природи тіл, їх взаємодій, а також і від характеру вихідного нерівноважного стану. Якщо система знаходиться в стані рівноваги, то в рівновазі знаходяться і окремі її макроскопічні частини. При незмінних зовнішніх умовах такий стан не змінюється з часом. Слід підкреслити, що незмінність у часі не є достатньою ознакою равновесности стану. Наприклад, поміщений в термостат ділянка електричного кола, по якому тече постійний струм, знаходиться в незмінному (стаціонарному) стані практично необмежений час. Однак цей стан нерівноважної: протікання струму супроводжується необоротним перетворенням енергії електричного струму в теплоту, що відводиться в термостат, в системі є градієнт температури. У стаціонарному нерівноважному стані можуть перебувати і все так звані відкриті системи .

Рівноважний стан повністю характеризується невеликим числом фізичних параметрів. Перш за все, це температура , Рівність значень якої для всіх частин системи є необхідною умовою термодинамічної рівноваги. (Існування температури - параметра, єдиного для всіх частин системи, що знаходиться в рівновазі, часто називається нульовим початком Т.) Стан однорідної рідини або газу повністю фіксується завданням будь-яких двох з трьох величин: температури Т, об'єму V і тиск р. Зв'язок між р, V і Т характерна для кожної даної рідини (газу) і називається рівнянням стану (Наприклад, Клапейрона рівняння для ідеального газу або Ван-дер-Ваальса рівняння ). У більш складних випадках для повної характеристики рівноважного стану можуть знадобитися і ін. Параметри (наприклад, концентрації окремих складових суміші газів, напруженість електричного поля, магнітна індукція).

Оборотні (квазістатичні) і незворотні процеси. У процесі переходу з одного рівноважного стану в інший, який може відбуватися під впливом різних зовнішніх впливів, система проходить через безперервний ряд станів, які не є, взагалі кажучи, рівноважними. Для реалізації процесу, що наближається за своїми властивостями до рівноважного, необхідно, щоб він протікав досить повільно. Але сама по собі повільність процесу ще не є достатньою ознакою його равновесности. Так, процес розрядки компенсатора через великий опір або дроселювання (див. Джоуля-Томсона ефект ), При якому газ перетікає з однієї судини в іншій через пористу перегородку під впливом перепаду тисків, можуть бути як завгодно повільними і при цьому істотно нерівновагими процесами. Рівноважний процес, представляючи собою безперервний ланцюг рівноважних станів, є оборотним - його можна зробити в зворотному напрямку, і при цьому в навколишньому середовищу не залишиться ніяких змін. Т. дає повне кількісне опис оборотних процесів , А для необоротних процесів встановлює лише певні нерівності і вказує напрям їх протікання.

Перший початок термодинаміки. Існують два принципово розрізняються способу зміни стану системи: перший пов'язаний з роботою системи по переміщенню на макроскопічні відстані навколишніх тіл (або роботою цих тіл над системою); другий - з повідомленням системи теплоти (або з відведенням теплоти) при незмінному розташуванні навколишніх тіл. У загальному випадку перехід системи з одного стану в інший пов'язаний з повідомленням системи деякої кількості теплоти D Q і здійсненням системою роботи D А над зовнішніми тілами. Як показує досвід, при заданих початковому і кінцевому станах D Q і D А істотно залежать від шляху переходу. Іншими словами, ці величини є характеристиками не окремої стану системи, а здійснюваного нею процесу. Перший початок термодинаміки стверджує, що якщо система здійснює термодинамічний цикл (тобто повертається в кінцевому рахунку в початковий стан), то загальна кількість теплоти, повідомлене системі протягом циклу, так само досконалої нею роботі.

Перший початок Т. є по суті вираз закону збереження енергії для систем, в яких істотну роль грають теплові процеси. Енергетична еквівалентність теплоти і роботи, тобто можливість виміру їх кількостей в одних і тих же одиницях і тим самим можливість їх порівняння була доведена дослідами Ю. Р. Майера (1842) і особливо Дж. Джоуля (1843). Перший початок Т. було сформульовано Майєром, а потім в значно більш ясною формі Г. Гельмгольцом (1847). Наведена вище формулювання першого початку рівнозначна, очевидно, твердження про неможливість вічного двигуна 1-го роду.

З першого початку слід, що в разі незамкнутого процесу (коли система не повертається у вихідне стан) різниця D Q - D А º D U хоча і не дорівнює, взагалі кажучи, нулю, але в усякому разі не залежить від шляху переходу між даними станами . Дійсно, довільний процес у зворотному напрямку утворює з кожним з прямих процесів замкнутий цикл, для якого зазначена різниця звертається в нуль. Таким чином, D U є приріст величини U, що має в кожному стані цілком певне значення, або, як кажуть, є функцією станів системи. Ця величина називається внутрішньою енергією (Або просто енергією) системи. Таким чином, з першого початку Т. витікає, що існує характеристична функція стану системи - її енергія. Якщо мова йде про однорідному тілі, яке здатне здійснювати роботу тільки при зміні обсягу, то D А = pdV і нескінченно малий приріст (диференціал) U одно:

dU = dQ - pdV, (1)

де dQ - нескінченно малий приріст теплоти, яка не є, однак, диференціалом якої-небудь функції. При фіксованому обсязі (dV = 0) вся повідомляється тілу теплота йде на приріст внутрішньої енергії, і тому, зокрема, теплоємність тіла при постійному об'ємі c v = (dU / dT) v. Вводячи іншу функцію станів H = U + pV ( ентальпію ), Диференціал якої

dH = dU + Vdp, (2)

можна отримати вираз для теплоємності, вимірюваної при постійному тиску: ср = (dH / dT) p. У разі ідеального газу, який описується рівнянням станів Клапейрона pV = nRT (n - число молей газу в об'ємі V, R - газова постійна ), Як вільна енергія, так і ентальпія певної маси газу залежать тільки від Т, що підтверджується, наприклад, відсутністю охолодження в процесі Джоуля - Томсона. Тому для ідеального газу cp - cv = nR.

Другий закон термодинаміки. Забороняючи вічний двигун 1-го роду, перший початок Т. не виключає можливості створення такої машини безперервної дії, яка була б здатна перетворювати в корисну роботу практично всю підводиться до неї теплоту (так званий вічний двигун 2-го роду). Однак весь досвід по конструюванню теплових машин, що був на початку 19 ст., Вказував на те, що ккд цих машин (відношення витраченої теплоти до отриманої роботі) завжди істотно менше одиниці: частина теплоти неминуче розсіюється в навколишнє середовище. С. Карно першим показав (1824), що ця обставина має принциповий характер, тобто будь-яка теплова машина повинна містити крім нагрівача (джерела теплоти) і робочого тіла, що здійснює термодинамічний цикл (наприклад, пара), також і холодильник, що має температуру, обов'язково нижчу, ніж температура нагрівача. Другий закон термодинаміки являє собою узагальнення виведення Карно на довільні термодинамічні процеси, що протікають в природі. Р. Клаузиус (1850) дав 2-му початку наступне формулювання: теплота не може мимоволі перейти від системи з меншою температурою до системи з більшою температурою. Незалежно в дещо іншій формі цей принцип висловив У. Томсон (Кельвін) в 1851: неможливо побудувати періодично діючу машину, вся діяльність якої зводилася б до підняття деякого вантажу (вчинення механічної роботи) і відповідному охолодженню теплового резервуара. Незважаючи на якісний характер цього твердження, воно призводить до далекосяжних кількісним наслідків.

Перш за все воно дозволяє визначити максимальний ккд теплової машини. Якщо машина працює на основі Карно циклу , То протягом ізотермічного контакту з нагрівачем (Т = T1) робоче тіло отримує кількість теплоти D Q 1, а на іншому ізотермічному ділянці циклу, перебуваючи в контакті з холодильником (Т = Т2), віддає йому кількість теплоти D Q 2. Ставлення D Q 2 / D Q 1 має бути одним і тим же у всіх машин з оборотним циклом Карно, у яких однакові відповідно температури нагрівачів і холодильників, і не може залежати від природи робочого тіла. Якби це було не так, то машину з більшою величиною зазначеного відносини можна було б змусити працювати в зворотному напрямку (оскільки цикли оборотні), приводячи її в дію за допомогою машини з меншою величиною відносини. Ця комбінована машина володіла б тим властивістю, що в ній теплота від холодильника передавалася б нагрівача без здійснення роботи. Згідно з 2-м початку Т. це неможливо, і тому відношення D Q 2 / D Q 1 в обох машин має бути однаковим. Зокрема, воно повинно бути тим же, що і в разі, коли робочим тілом є ідеальний газ. Тут це відношення легко може бути знайдено, і, таким чином, виявляється, що для всіх оборотних циклів Карно

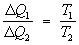. (3)

Цей вислів називається пропорцією Карно. В результаті для всіх машин з оборотним циклом Карно ккд максимальний і дорівнює h = (T1 - T2) / T1. У разі, якщо цикл незворотній, то ккд виявляється менше цієї величини. Необхідно підкреслити, що пропорція Карно і ккд циклу Карно мають вказаний вид тільки в тому випадку, якщо температура виміряна в абсолютній температурній шкалі. Пропорція Карно покладена в основу визначення абсолютної температурної шкали (див. температурні шкали ). Наслідком 2-го початку Т. (пропорції Карно) є існування ентропії як функції станів. Якщо ввести величину S, зміна якої при ізотермічному оборотному повідомленні системи кількості теплоти D Q є D S = DQ / T, то повний приріст S в циклі Карно дорівнюватиме нулю; на адіабатичних ділянках циклу D S = 0 (так як D Q = 0), а зміни на ізотермічних ділянках компенсують один одного. Повний приріст S виявляється рівним нулю і при здійсненні довільного оборотного циклу, що доводиться розбиттям циклу на послідовність нескінченно тонких циклів Карно (з малими ізотермічними ділянками). Звідси випливає (як і в разі внутрішньої енергії), що ентропія S є функцією стану системи, тобто зміна ентропії не залежить від шляху переходу. Використовуючи поняття ентропії, Клаузіус (1876) показав, що вихідна формулювання 2-го початку Т. повністю еквівалентна наступній: існує функція стану системи, її ентропія S, приріст якої при оборотному повідомленні системи теплоти одно

dS = dQ / T; (4)

при реальних (необоротних) адіабатичних процесах ентропія зростає, досягаючи максимальне значення в стані рівноваги.

Термодинамічні потенціали. Визначення ентропії дозволяє написати наступні вирази для диференціалів внутрішньої енергії та ентальпії:

dU = TdS - pdV, dH = TdS + Vdp. (5)

Звідси видно, що природними незалежними параметрами стану для функцій U і Н є відповідно пари S, V і S, р. Якщо ж замість ентропії як незалежний параметр використовується температура, то для опису системи зручніші вільна енергія ( Гельмгольцева енергія , Або ізохорно-ізотермічний потенціал) F = U - TS (для змінних Т і V) і термодинамічний потенціал G = Н - TS для змінних Т і р ( гиббсова енергія , Або ізобарно-ізотермічний потенціал), диференціали яких рівні

dF = - SdT - pdV, dG = -SdT + Vdp. (6)

Функції станів U, Н, F і G називаються потенціалами термодинамічними системи для відповідних пар незалежних змінних. Метод термодинамічних потенціалів (Дж. Гіббс, 1874-1878), заснований на спільному застосуванні 1-го і 2-го почав Т., дозволяє отримати ряд важливих термодинамічних співвідношень між різними фізичними властивостями системи. Так, використання незалежності других змішаних похідних від порядку диференціювання приводить до зв'язку між теплоємність ср і cv, коефіцієнтом теплового розширення 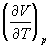і ізотермічним коефіцієнтом стиснення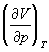

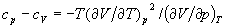
до співвідношення між ізотермічним і адіабатичним коефіцієнтами стиснення 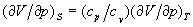і т. п. З умови, що ізольована система в рівноважному стані володіє максимальним значенням ентропії, випливає умова мінімальності термодинамічних потенціалів в рівноважному стані по відношенню до довільних малих відхилень від рівноваги при фіксованих значеннях відповідних незалежних змінних. Це призводить до важливих нерівностей (умовам стійкості), зокрема

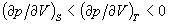, Cp> cv> 0 (див. стійкість термодинамічна ).

Третій закон термодинаміки. Ентропія визначається згідно 2-му початку Т. диференціальним співвідношенням (4), тобто визначається з точністю до постійного доданка, яка хоч і не залежить від температури, але могло б бути різним для різних тіл в стані рівноваги. Відповідні невизначені доданки існують і у термодинамічних потенціалів. В. Нернст (1906) на основі своїх електрохімічних досліджень прийшов до висновку, що ці складові повинні бути універсальними: вони не залежать від тиску, агрегатного стану і інших характеристик речовини. Цей новий, наступний з досвіду принцип зазвичай називається третім початком термодинаміки або теплової теоремою Нернста. М. Планк (1911) показав, що воно рівносильне умові: ентропія всіх тіл в стані рівноваги прагне до нуля в міру наближення до абсолютного нуля температури, оскільки універсальну константу в ентропії можна покласти рівною нулю. З 3-го початку Т. слід, зокрема, що коефіцієнт теплового розширення, Ізохоричний коефіцієнт тиску і питомі теплоємності c p і c v звертаються в нуль при T ® 0. Необхідно відзначити, що 3-е початок Т. і витікаючі з нього слідства не відносяться до систем, що знаходяться в так званому загальмованому стані. Прикладом такої системи є суміш речовин, між якими можливі хімічні реакції, але вони загальмовані - швидкість реакцій при низьких температурах дуже мала. Іншим прикладом може служити швидко заморожений розчин, який при низькій температурі повинен був би расслоиться на фази, але процес розшарування при низьких температурах практично не відбувається. Такі стани у багатьох відношеннях подібні рівноважним, проте їх ентропія не звертається до нуль при Т = 0.

Застосування термодинаміки. Важливими областями застосування Т. є теорія рівноваги хімічного і теорія фазового рівноваги , Зокрема рівноваги між різними агрегатними станами і рівноваги при розшаруванні на фази сумішей рідин і газів. У цих випадках в процесі встановлення рівноваги істотну роль грає обмін частками речовини між різними фазами, і при формулюванні умов рівноваги використовується поняття хімічного потенціалу . Постійність хімічного потенціалу замінює умова постійності тиску, якщо рідина або газ знаходяться в зовнішньому полі, наприклад поле тяжіння. Методи Т. ефективно застосовуються при вивченні тих явищ природи, в яких істотну роль грають теплові ефекти. У Т. прийнято виділяти розділи, які стосуються окремих наук і до техніки (хімічна Т., технічна Т. і т. Д.), А також до різних об'єктів дослідження (Т. пружних тіл, Т. діелектриків, магнетиків, надпровідників, плазми , випромінювання, атмосфери, води та ін.).

З'ясування статистичної природи ентропії привело до побудови термодинамічної теорії флуктуацій (А. Ейнштейн , 1910) і до розвитку термодинаміки нерівноважних процесів .

Літ .: Зоммерфельд А., Термодинаміка і статистична фізика, М., 1955; Леонтович М. А., Введення в термодинаміку, 2 вид., М.-Л., 1952; Ландау Л. Д., Ліфшиц Е. М., Статистична фізика, 2 вид., М., 1964 (Теоретична фізика, т. 5); Другий закон термодинаміки. Сб., М.-Л., 1934; Епштейн П. С., Курс термодинаміки, пров. з англ., М.-Л., 1948; Ван-дер-Ваальса І. Д., Констамм Ф., Курс термостатики, пров. з нім., М., 1936; Кубо Р., Термодинаміка, пров. з англ., М., 1970; Термодинаміка. Термінологія. Сб., М., 1973.

Г. М. Еліашберг.