1. Методи обчислення і ефект ребер
2. площинний метод
3. Алгоритм обчислення площинного ухилу
4. Приклад обчислення площинного ухилу
5. геодезичний метод
6. Перетворення геодезичних координат
7. обчислення ухилу
8. Використання графічного процесора (GPU)
9. Довідкова інформація

Доступно з ліцензією Spatial Analyst.

Доступно з ліцензією 3D Analyst.

інструмент ухил визначає крутизну в кожному осередку растрової поверхні. Чим менше значення ухилу, тим більш плоскою є земна поверхня; чим більше значення ухилу, тим більше круті схили розташовані на поверхні.

Вихідний растр ухилів може бути обчислений в двох різних одиницях виміру, в градусах або у відсотках ( 'відсоток підйому'). Відсоток підйому можна краще зрозуміти, якщо ви розглядаєте його як підйом, поділений на пробіг (спуск), помножений на 100. Розглянемо трикутник B на малюнку внизу. Коли кут дорівнює 45 градусам, підйом дорівнює пробігу (спуску), а відсоток підйому дорівнює 100 відсоткам. У міру того, як кут нахилу наближається до вертикального (90 градусів), як в трикутнику C, відсоток підйому прагне до нескінченності.

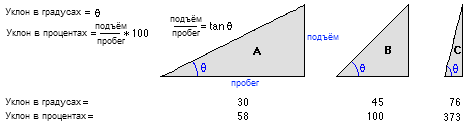
Порівняння значень ухилів в градусах і відсотках.

Інструмент Ухил найчастіше працює з набором даних висот, як показано на наступних малюнках. Більш круті схили позначені на вихідному растрі ухилу більш темним коричневим.

Інструмент також може використовуватися з іншими типами безперервних даних, наприклад, чисельність населення, для виявлення різких змін значення.

Методи обчислення і ефект ребер

Для обчислення ухилу є два методи. Ви можете вибрати метод обчислення Площинний або Геодезичний, використовуючи параметр Метод.

Для площинного методу, ухил вимірюється як максимальне співвідношення зміни значень комірки і її безпосереднього оточення. Розрахунок виконується на проектуватися площині при використанні декартової системи координат 2D. Значення ухилу обчислюється з використанням методики усередненого максимуму (Burrough, 1998).

За геодезичного методу обчислення будуть виконуватися в декартовій системі координат 3D урахуванням форми земної поверхні у вигляді еліпсоїда. Значення ухилу обчислюється виміром кута між топографічної поверхнею і базовим датум.

Площинні та геодезичні обчислення виконуються за допомогою околиці розміром 3 на 3 осередки (плаваюче вікно). Для кожної околиці, якщо обробляється (центральна) осередок має значення NoData, вихідне значення буде NoData. Для обчислень також необхідно, щоб не менше семи навколишніх осередків мали допустимі значення. Якщо менше семи осередків мають коректні значення, обчислення не проводиться, а вихідним значенням оброблюваної осередку буде NoData.

Осередки в найбільш віддалених рядках і шпальтах вихідного растру отримають значення NoData. Це відбувається тому, що вздовж кордону вхідного набору даних у осередків немає достатньої кількості сусідів.

площинний метод

Для кожного осередку інструмент обчислює максимальну ступінь зміни в значенні z між конкретною осередком і сусідніми з нею осередками. По суті, максимальний ступінь зміни в значеннях висоти на одиницю відстані між осередком і вісьмома сусідніми з нею осередками визначає самий крутий спуск вниз по схилу з осередку.

Алгоритм обчислення площинного ухилу

Ухил визначає ступінь зміни (дельту) поверхні в горизонтальному (dz / dx) і вертикальному (dz / dy) напрямках з центрального осередку. Базовий алгоритм, який використовується для обчислення ухилу, виглядає так:

slope_radians

= ATAN (√ ([dz / dx] 2 + [dz / dy] 2))

Ухил зазвичай вимірюється в градусах з використанням наступного алгоритму:

= ATAN (√ ([dz / dx] 2 + [dz / dy] 2)) * 57.29578

Показане тут значення 57,29578 - це скорочена версія результату операції 180 / pi.

Алгоритм ухилу може бути проінтерпретувати також наступним чином:

slope_degrees

= ATAN (rise_run) * 57.29578

Горизонтальну і вертикальну дельти визначають значення центрального осередку і восьми сусідніх з нею осередків. Сусідні комірки позначаються буквами від a до i, при цьому буква e позначає комірку, для якої обчислюється ухил.

Вікно сканування поверхні

Ступінь зміни у напрямку x для осередку 'e' обчислюється за допомогою наступного алгоритму:

[dz / dx] = ((з + 2 f + i) * 4 / wght1 - (a + 2 d + g) * 4 / wght2) / (8 * x_cellsize)

• де:

  wght1 і wght2 є горизонтально зваженим числом коректних осередків.

  Наприклад, якщо:

  • c, f і i мають коректні значення, wght1 = (1 + 2 * 1 + 1) = 4.
  • i є NoData, wght1 = (1 + 2 * 1 + 0) = 3.
  • f є NoData, wght1 = (1 + 2 * 0 + 1) = 2.

  Аналогічна логіка застосовується до wght2, за винятком того, що сусідніми місцями розташування є a, d і g.

Ступінь зміни у напрямку y для осередку 'e' обчислюється за допомогою наступного алгоритму:

[dz / dy] = ((g + 2 h + i) * 4 / wght3 - (a + 2 b + с) * 4 / wght4) / (8 * y_cellsize)

Приклад обчислення площинного ухилу

Як приклад буде обчислено значення ухилу центрального осередку ковзного вікна.

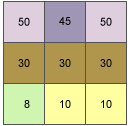
Приклад вхідних даних ухилом

Ступінь зміни для центрального осередку 'e' у напрямку x:

[dz / dx] = ((з + 2 f + i) * 4 / wght1 - (a + 2 d + g) * 4 / wght2) / (8 * x_cellsize) = ((50 + 60 + 10) * 4 / (1 + 2 + 1) - (50 + 60 + 8) * 4 / (1 + 2 + 1)) / (8 * 5) = (120 - 118) / 40 = 0.05

Ступінь зміни для центрального осередку 'e' у напрямку y:

[dz / dy] = ((g + 2 h + i) * 4 / wght3 - (a + 2 b + с) * 4 / wght4) / (8 * y_cellsize) = ((8 + 20 + 10) * 4 / (1 + 2 + 1) - (50 + 90 + 50) * 4 / (1 + 2 + 1)) / (8 * 5) = (38 - 190) / 40 = -3.8

З огляду на ступінь зміни в напрямку x і y, ухил для центрального осередку e обчислюється з використанням наступного алгоритму:

= √ ([dz / dx] 2 + [dz / dy] 2) = √ ((0.05) 2 + (-3.8) 2) = √ (0.0025 + 14.44) = 3.80032 slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762

Цілочисельне значення ухилу для осередку 'e' становить 75 градусів.

Приклад вихідних даних ухилом

геодезичний метод

При геодезичному методі ухил поверхні вимірюється в геоцентричної 3D системі координат - також називається системою координат Earth Centered, Earth Fixed (ECEF) - з урахуванням еліпсоїдної форми землі. Проекція набору даних на результати обчислень не впливає. При цьому використовуються одиниці виміру z вхідного растру, якщо вони задані в просторової прив'язки. Якщо в просторової прив'язки вхідних даних не задані одиниці виміру z, необхідно зробити це за допомогою параметра завдання z-одиниць. Геодезичний метод дає більш точний результат, ніж площинний.

Перетворення геодезичних координат

Система координат ECEF є 3D правобічної Декартовой системою координат з центром землі в якості початкової точки, в якій будь-який пункт представлено координатами X, Y і Z. На наступному малюнку наводиться приклад цільового місця розташування T, вираженого в геоцентричних координатах.

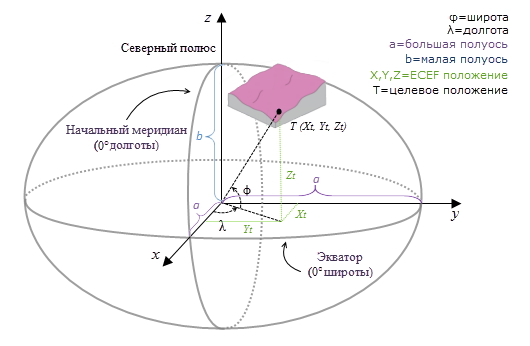
Растр поверхні трансформуються з вхідних системи координат в 3D геоцентричну систему координат.

В геодезичних обчисленнях використовуються координати X, Y, Z, які обчислюються на основі геодезичних координат (широта φ, довгота λ, висота h). Якщо система координат вхідного растру поверхні є системою координат проекції, растр спочатку перепроеціруется в географічну систему координат, в якій кожне місце розташування має геодезичні координати, потім він перетворюється в систему координат ECEF. Висота h (z-значення) є еліпсоїдної висотою, заснованої на поверхні еліпсоїда. Див. Ілюстрацію нижче.

еліпсоїдальної висота

Для перетворення геодезичних координат (широта φ, довгота λ, висота h) в координати ECEF використовуються наступні формули:

= (N (φ) + h) cos φ cos λ Y = (N (φ) + h) cos φ sin λ Z = (b 2 / a 2 * N (φ) + h) sin φ

• , Де:
  • N (φ) = a 2 / √ (a 2cos φ 2 + b 2sin φ 2)
  • φ = широта
  • λ = довгота
  • h = еліпсоїдальної висота
  • a = велика піввісь еліпсоїда
  • b = мала піввісь еліпсоїда

Еліпсоїдна висота h в наступних формулах дається в метрах. Якщо z-значення вхідного растру дані в інших одиницях виміру, вони будуть перетворені в метри.

обчислення ухилу

Геодезичний ухил є кутом між топографічної поверхнею і поверхнею еліпсоїда. Будь-яка поверхня, паралельна поверхні еліпсоїда, має ухил 0. Щоб обчислити ухил в кожному місцезнаходження, навколо оброблюваної осередку створюється площину околиці розміром 3 x 3 осередки, за методом найменших квадратів. Найкраще відповідність за методом найменших квадратів мінімізує суму квадратів різниці (dzi) між реальним і підібраним z-значенням. Приклад наведено на малюнку нижче.

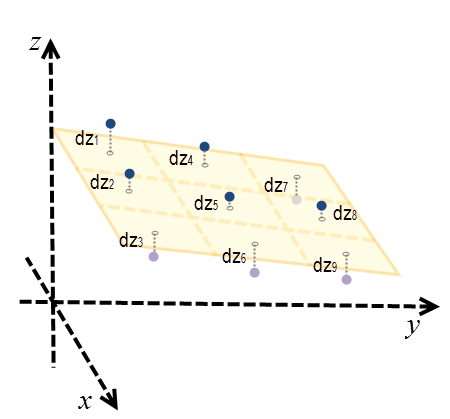
Приклад використання методу найменших квадратів

Тут площину представлена ​​у вигляді z = Ax + By + C. Для кожного центру осередки, dzi є різницею між реальним z-значенням і підібраним.

Найкраще відповідність площині досягається, коли Σ9i = 1dzi2 мінімальна.

Після підгонки площині, в місці розташування осередку обчислюється нормаль до поверхні. В тому самому розташуванні обчислюється нормаль еліпсоїда, перпендикулярна площині, що проходить по дотичній до поверхні еліпсоїда.

Обчислення геодезичного ухилу

Ухил, в градусах, обчислюється за кутом між нормаллю до еліпсоїда і нормаллю до топографічної поверхні, який тут позначається як β. Згідно малюнку вище, кут α є геодезичним ухилом, що відповідає куту β, відповідно до закону подібної геометрії.

Для обчислення ухилу у відсотках використовується наступна формула:

Slope_PercentRise

= ATAN (β) * 100%

Використання графічного процесора (GPU)

При використанні геодезичного методу, продуктивність інструменту значно підвищується якщо використовуються GPU певних моделей. Додаткові відомості про підтримку цього механізму, його налаштування і включення см. В розділі Робота GPU з Spatial Analyst .

Довідкова інформація

Burrough, PA, and McDonell, RA, 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.

Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.

David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.

пов'язані теми