1. глава 9
2. 2. Логічний КВАДРАТ
3. 3. КАТЕГОРИЧНИЙ СИЛОГІЗМ

<<< ОГЛАВЛЕHІЕ >>>

глава 9

1. Категоричне висловлювання

При розгляді способів утворення складних висловлювань з простих внутрішню будову простих висловлювань до уваги не приймалося. Вони бралися як нерозкладних атоми, що володіють тільки одним властивістю: бути істинними або помилковими. Прості висловлювання не випадково іноді іменуються атомарними: з них, як з елементарних цеглинок, з допомогою логічних зв'язок "і", "або" і т.п. будуються різноманітні складні ( "молекулярні") висловлювання.

Тепер слід зупинитися на питанні про внутрішню будову, або внутрішню структуру, самих простих висловлювань: з яких конкретних частин вони складаються і як ці частини пов'язані між собою.

Відразу ж потрібно підкреслити, що прості висловлювання можуть розкладатися на складові частини по-різному. Результат розкладання залежить від мети, заради якої воно здійснюється, тобто від тієї теорії логічного висновку (логічного слідування), в рамках якої аналізуються такі висловлювання.

Далі буде розглядатися лише один різновид простих висловлювань - категоричні висловлювання, за традицією звані також категоричними судженнями.

Особливий інтерес до категоричних висловлювань пояснюється перш за все тим, що з дослідження їх логічних зв'язків почався розвиток логіки як науки. Крім того, висловлювання цього типу широко використовуються в наших міркуваннях.

Категоричне висловлювання - це висловлювання, в якому стверджується або заперечується наявність якоїсь ознаки у всіх або деяких предметів даного класу.

Наприклад, в висловлюванні "Все динозаври вимерли" всім динозаврам (або, що те ж саме, кожному з динозаврів) приписується ознака "бути вимерлими". У висловлюванні "Деякі динозаври літали" здатність літати приписується деяким динозаврам. У висловлюванні "Все років комети не астероїди" заперечується наявність ознаки "бути астероїдом" у кожної з комет. У висловлюванні "Деякі тварини не є травоїдними" заперечується травоїдність деяких тварин.

Якщо відволіктися від кількісної характеристики, що міститься в категоричне висловлюванні і виражається словами "все" і "деякі", то вийде два варіанти таких висловлювань: позитивну і негативну. Їх структура:

"S є Р" і "S не є Р",

де буква S представляє ім'я того предмета, про який йде мова у висловленні, а буква Р - ім'я ознаки, властивого або не характерного для цього предмету.

Предмет, про який ідеться в категоричне висловлюванні, називається суб'єктом, а його ознака - предикатом. Суб'єкт і предикат називаються термінами категоричного висловлювання і з'єднуються між собою зв'язками "є" або "не є" ( "є" або "не є" тощо). Наприклад, в висловлюванні "Сонце є зірка" термінами є імена "Сонце" і "зірка" (перший з них - суб'єкт висловлювання, другий - його предикат), а слово "є" - зв'язка.

Прості висловлювання типу "S є (не є) Р" називаються атрибутивними: у них здійснюється атрибуція (приписування) якогось властивості предмету.

Атрибутивними висловлювань протистоять висловлювання про відносини, в яких встановлюються відносини між двома або більшою кількістю предметів: "Три менше п'яти", "Київ більше Одеси", "Весна краще осені", "Париж знаходиться між Москвою і Нью-Йорком" і т.п . Висловлювання про відносини відіграють істотну роль в науці, особливо в математиці. Вони не зводяться до категоричних висловлювань, оскільки відносини між кількома предметами (такі, як "одно", "любить", "тепліше", "знаходиться між" і т.д.) не зводяться до властивостей окремих предметів.

У категоричному висловлюванні не просто встановлюється зв'язок предмета і ознаки, а й дається певна кількісна характеристика суб'єкта висловлювання. У висловлюваннях типу "Всі S є (не є) Р" слово "все" означає "кожен з предметів відповідного класу". У висловлюваннях типу "Деякі S є (не є) Р" слово "деякі" вживається в невиключає сенсі і означає "деякі, а може бути все". У виключає сенсі слово "деякі" означає "тільки деякі", або "деякі, але не всі". Різниця між двома смислами цього слова можна продемонструвати на прикладі висловлювання "Деякі зірки є зірки". У невиключає сенсі воно означає "Деякі, а можливо і всі зірки є зірки" і є, очевидно, істинним. В виключає ж сенсі це висловлювання означає "Лише деякі зірки є зірками" і є явно хибним.

У категоричних висловлюваннях стверджується або заперечується приналежність якихось ознак розглянутих предметів і вказується, чи йде мова про всі ці предмети або ж про деякі з них. Можливі, таким чином, чотири види категоричних висловлювань:

Всі S є Р - общеутвердительное висловлювання,
Деякі S є Р - частноутвердітельное висловлювання,
Всі S не є Р - общеотріцательное висловлювання,
Деякі S не є Р - частноотріцательное висловлювання.

Категоричні висловлювання можна розглядати як результати підстановки якихось імен в наступні вирази з "пробілами" (многоточиями): "Все ... є ...", "Деякі ... є ...", "Все ... не є ... "і" Деякі ... не є ... ". Кожне з цих виразів є логічною постійною (логічною операцією), що дозволяє з двох імен отримати висловлювання. Наприклад, підставляючи замість крапок імена "літаючі" і "птахи", отримуємо, відповідно, такі висловлювання: "Все літаючі є птахи", "Деякі літаючі є птахи", "Все літаючі не їсти птиці" і "Деякі літаючі не їсти птиці" . Перше і третє висловлювання є неправдивими, а друге і четверте - істинними.

Арістотель тлумачив розглядаються чотири висловлювання саме як логічні постійні, які не мають самостійного змісту і дозволяють з двох володіють змістом імен отримувати змістовні, є істинними або помилковими висловлювання.

У традиційній логіці передбачалося також, що імена, що підставляються замість крапок (або змінних, якщо вони використовуються замість крапок), не повинні бути поодинокими або порожніми. Інакше кажучи, висловлювання типу "Платон - людина", "Все золоті гори - це гори" не належать до категоричних в традиційному сенсі, оскільки "Платон" - одиничне ім'я, а "золоті гори" - пусте ім'я.

Позначимо оборот "Все ... є ..." буквою а, оборот "Деякі ... є ..." буквою i (перші голосні літери латинського слова affirmo - стверджую), оборот "Все ... не є ... "буквою е і оборот" Деякі ... не є ... "буквою про (голосні літери латинського слова nego - заперечую).

SaP - "Всі S є Р" - "Все рідини пружні",
SiP - "Деякі S є Р" - "Деякі тварини говорять",
SeP - "Всі S не є Р" - "Все дельфіни не є риби",
SoP - "Деякі S не є Р" - "Деякі метали не є рідини".

Відносини між термінами в чотирьох видах категоричних висловлювань представляються за допомогою кіл Ейлера наступним чином:

2. Логічний КВАДРАТ

Деякі відносини між чотирма видами категоричних висловлювань графічно представляються так званим логічним квадратом.

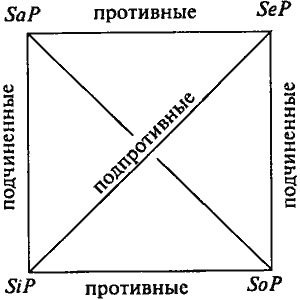
Ухвалені закони суперечать висловлювання (SaP і SoP; SeP і SiP) не можуть бути одночасно істинними і помилковими; якщо одне з них істинно, то інше брехливо. Так, якщо висловлювання "Усі кити дихають легенями" істинно, то висловлювання "Деякі кити не дихають легенями" помилково. Якщо висловлювання "Деякі ведмеді - НЕ бурі" істинно, то висловлювання "Усі ведмеді - бурі" помилково.

Неприємні висловлювання (SaP і SeP), на відміну від суперечать, можуть разом бути помилковими, але не можуть бути разом істинними. Так, висловлювання "Усі спортсмени - гросмейстери" і "Жоден спортсмен не гросмейстер" обидва хибні. Оскільки висловлювання "У всіх людей є голови" істинно, то висловлювання "У жодного людини немає голови" помилково; і якщо висловлювання "Усі метали не є газами" істинно, то висловлювання "Усі метали - гази" помилково.

Подпротівние висловлювання (SiP і SoP) не можуть бути одночасно хибними, але можуть бути одночасно істинними. Так, якщо висловлювання "Деякі вівці - хижаки" помилково, то висловлювання "(Щонайменше) деякі вівці не є хижаками" істинно. Висловлювання ж «Деякі спортсмени - футболісти" і "Деякі спортсмени не футболісти" обидва істинні.

Що стосується підпорядкування перебувають попарно висловлювання SaP і SiP, SeP і SoP. З підпорядковує висловлювання логічно випливає підлегле: з SaP випливає SiP і з SeP випливає SoP. Це означає, що з істинності підпорядковує висловлювання логічно випливає істинність підлеглого, і з хибності підлеглого слід хибність підпорядковує. Наприклад, з висловлювання "Усі кити є ссавцями" слід висловлювання "Деякі кити ссавці", а з висловлювання "Усі метали не є стисливими" слід висловлювання "Деякі метали не стискувані".

Ще раз підкреслимо, що суперечать один одному висловлювання "Усі S є Р" і "Деякі S не є Р" та слова "Всі S не є Р" і "Деякі S є Р". Висловлювання ж "Всі S є Р" і "Всі S не є Р", а також висловлювання "Деякі S є Р" і "Деякі S не є Р" не суперечать один одному.

Логічні зв'язки категоричних висловлювань, що подаються логічним квадратом, можна уявити також у формі безпосередніх умовиводів, тобто умовиводів з однієї посилки.

Суперечать один одному висловлювання "Усі S є Р" і "Деякі S не є Р", а також висловлювання "Усі S не є Р" і "Деякі S є Р". Це означає, що є правильними такі, зокрема, безпосередні умовиводи:

Всі S є Р.

З висловлювання "Усі сови - птахи" безпосередньо випливає висловлювання "Невірно, що деякі сови не є птахами".

Деякі S не є Р.

З висловлювання "Деякі вчені не хіміки" безпосередньо випливає висловлювання "Невірно, що всі вчені хіміки".

Всі S не є Р.

З висловлювання "Усі кити НЕ риби" безпосередньо випливає висловлювання "Невірно, що деякі кити - риби".

Деякі S є Р.

З висловлювання "Деякі рідини пружні" безпосередньо випливає висловлювання "Невірно, що всі рідини непружним".

Неприємні висловлювання (SaP і SeP) не можуть бути разом істинними.

Всі S є Р.

З висловлювання "Усі літаючі мають крила" безпосередньо випливає висловлювання "Невірно, що всі літаючі не мають крил".

Всі S не є Р.

З висловлювання "Усі категоричні висловлювання не є умовними" безпосередньо випливає висловлювання "Невірно, що всі категоричні висловлювання - умовні".

З підпорядковує висловлювання логічно випливає підлегле:

Всі S є Р.

З висловлювання "Усі люди дихають легенями" безпосередньо випливає висловлювання "(Щонайменше) деякі люди дихають легенями".

Всі S не є Р.

З висловлювання "Усі тигри не птахи" безпосередньо випливає висловлювання "Деякі тигри не птахи".

3. КАТЕГОРИЧНИЙ СИЛОГІЗМ

Категоричний силогізм (або просто: силогізм) - це дедуктивний умовивід, в якому з двох категоричних висловлювань виводиться нове категоричне висловлювання.

Логічна теорія такого роду умовиводів називається силлогистикой. Вона була створена ще Аристотелем і довгий час служила зразком логічної теорії взагалі.

У силогістиці вираження "Все ... є ...", "Деякі ... є ...", "Все ... не є ..." і "Деякі ... не є ..." розглядаються як логічні постійні, тобто беруться як єдине ціле. Це не висловлювання, а певні логічні форми, з яких виходять висловлювання шляхом підстановки замість крапок якихось імен. Підставляються імена називаються термінами силогізму.

Істотним є таке традиційне обмеження: терміни силогізму не повинні бути порожніми або негативними.

Прикладом силогізму може бути:

Всі рідини пружні.
Вода - рідина.

У кожному силогізмі має бути три терміна: менший, більший і середній.

Меншим терміном називається суб'єкт висновку (в прикладі таким терміном є термін "вода").

Великим терміном іменується предикат висновку ( "пружна"). Термін, присутній у посилках, але відсутній у висновку, називається середнім ( "рідина"). Менший термін позначається зазвичай літерою S, більший - буквою Р і середній - буквою М. Посилка, в яку входить більший термін, називається більшої. Посилка з меншим терміном називається меншою. Велика посилка записується першою, менша - другий. Логічна форма наведеного силогізму така:

Все М є Р.
Всі S є М.

Залежно від положення середнього терміна в посилках (є він суб'єктом чи предикатом в більшій і меншій посилках) розрізняються чотири фігури силогізму. Схематично фігури зображаються так:

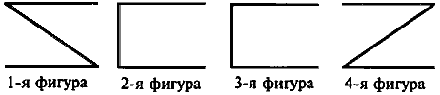
За схемою першої фігури побудований силогізм:

Всі птахи (М) мають крила (Р).
Все страуси (S) - птиці (М).

За схемою другої фігури побудований силогізм:

Всі риби (Р) дихають зябрами (М).
Кити (S) не дихають зябрами (М).

За схемою третьої фігури побудований силогізм:

Все бамбуки (М) цвітуть один раз в житті (Р).
Все бамбуки (М) - багаторічні рослини (S).

За схемою четвертої фігури побудований силогізм:

Всі риби (Р) плавають (М).
Всі плаваючі (М) живуть у воді (S).

Посилками та висновками силогізмів можуть бути категоричні судження чотирьох видів: SaP, SiP, SeP і SoP.

Модусами силогізму називаються різновиди фігур, що відрізняються характером посилок і висновку.

Всього з точки зору всіляких поєднань посилок і укладання в кожній фігурі налічується 64 модусу. У чотирьох фігурах 4 × 64 = 256 модусів.

Силогізми, як і всі дедуктивні умовиводи, діляться на правильні і неправильні. Завдання логічної теорії силогізму - систематизувати правильні силогізми, вказати їх відмінні риси.

З усіх можливих модусів силогізму тільки 24 модусу є правильними, по шість в кожній фігурі. Ось традиційно прийняті назви правильних модусів перших двох фігур:

1-я фігура: Barbara, Celarent, Darii, Ferio, Barbari, Celaront;
2-я фігура: Cesare, Camestres, Festino, Baroco, Cesaro, Camestros.

У кожному з цих назв містяться три голосних букви. Вони вказують, які саме категоричні висловлювання використовуються в модусі як його посилок і висновку. Так, назва Celarent означає, що в цьому модусі першої фігури більшої посилкою є общеотріцательное висловлювання (SeP), меншою - общеутвердительное (SaP) і укладенням - общеотріцательное висловлювання (SeP).

З 24 правильних модусів силогізму 5 є ослабленими: висновками в них є частноутвердітельние або частноотріцательние висловлювання, хоча в разі інших модусів ці ж посилки дають общеутвердітельние або общеотріцательние укладення (пор. Модуси Cesare і Cesaro другої фігури). Якщо відкинути ослаблені модуси, залишається 19 правильних модусів силогізму.

Для оцінки правильності силогізму можуть використовуватися кола Ейлера, що ілюструють відносини між обсягами імен.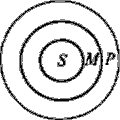

Візьмемо, для прикладу, силогізм:

Всі метали (М) ковки (Р).
Залізо (S) - метал (М).

Відносини між трьома термінами цього силогізму (модус Barbara) представляються трьома концентричними колами. Ця схема інтерпретується так: якщо все М (метали) входять в обсяг Р (ковких тел), то з необхідністю S (залізо) увійде в обсяг Р (ковких тел), що і стверджується у висновку "Залізо ковке".

Інший приклад силогізму: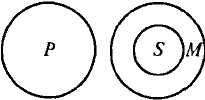

Всі риби (Р) не мають пір'я (М).
У всіх птахів (S) має плавці (М).

Відносини між термінами даного силогізму (модус Cesare) представлені на малюнку. Він тлумачиться так: якщо все S (птиці) входять в обсяг М (мають пір'я), а М не має нічого спільного з Р (риби), то у S (птиці) немає нічого спільного з Р (риби), що і затверджується в ув'язненні.

Приклад неправильного силогізму: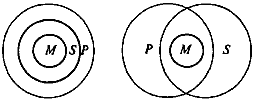

Всі тигри (М) - ссавці (Р).
Всі тигри (М) - хижаки (S).

Відносини між термінами даного силогізму можуть бути представлені двояко, як це показано на малюнку. І в першому, і в другому випадках все М (тигри) входять в обсяг Р (ссавці) і все М входять також в обсяг S (хижаки). Це відповідає інформації, що міститься в двох посилках силогізму. Але відношення між обсягами Р і S може бути двояким. Охоплюючи М, обсяг S може повністю входити в обсяг Р або обсяг S може лише перетинатися з об'ємом Р. В першому випадку можна було б зробити загальний висновок "Все хижаки - ссавці", але в другому випадку правомірно тільки приватна висновок "Деякі хижаки - ссавці ". Інформації, що дозволяє зробити вибір між цими двома варіантами, в посилках не міститься. Значить, ми не маємо права робити загальний висновок. Силогізм не є правильним.

У сілогізм, як и у всякому дедуктивний умовівід, у висновка НЕ ​​может містітіся інформація, відсутня в посилках. Висновок тільки розгортає інформацію посилок, але не може привносити нову інформацію, відсутню в них.

У звичайних міркуваннях нерідкі силогізми, в яких не виражається явно одна з посилок або висновок. Такі силогізми називаються ентимемами. Приклади ентімем: "Щедрість заслуговує похвали, як і будь-яка чеснота", "Він - вчений, тому цікавість йому не чуже", "Гас - рідина, тому він передає тиск на всі боки рівномірно" і т.п. У першому випадку опущена менша посилка "Щедрість - це чеснота", у другому - велика посилка "Всякому вченому не чуже цікавість", в третьому - знову-таки велика посилка "Всяка рідина передає тиск на всі боки рівномірно".

Для оцінки правильності міркування в ентимема слід відновити її в повний силогізм.