Рикк а ти зрівняні е ня, звичайне диференціальне рівняння 1-го порядку виду

, (*)

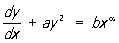де а, b, а - постійні. Це рівняння вперше досліджувалося Я. Риккати (1724); окремі окремі випадки розглядалися раніше. Д. Бернуллі встановив (1724-25), що рівняння (*) інтегрується в елементарних функціях, якщо а = - 2 або а = - 4 kl (2 k - 1), де k - ціле число. Як довів Ж. Лиувилль (1841), при інших значеннях а рішення рівняння (*) не можна виразити в квадратурі від елементарних функцій; спільне рішення його може бути записано за допомогою циліндричних функцій . диференціальне рівняння

,

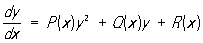де Р (х), Q (x), R (x) - безперервні функції, називається загальним Р. у. [На відміну від нього рівняння (*) називається спеціальним Р. у.]. При Р (х) = 0 загальне Р. у. є лінійним диференціальним рівнянням, при R (x) = 0 - так званим Бернуллі рівнянням , Які інтегруються в кінцевому вигляді. Вивчено також інші випадки інтегрованості загального Р. у.

Літ .: Камке Е., Довідник по звичайних диференціальних рівнянь, пров. з нім., 4 видавництва., М., 1971.